Matemática, ilusiones y humor
Cientificólogos
Quiero comenzar por felicitar a los/las autores y lectores de este medio, por tratarse de un tiempo especialmente interesante para los científicos (aunque no puedo dejar de recordar al historiador Eric Hobsbawm cuando señaló que hay una maldición china que dice ‘ojalá te toquen vivir tiempos interesantes’).
Sin duda es una época en la que el eje de la discusión, el debate, la polémica, la controversia y una larga lista de sinónimos que no tiene sentido nombrar (salvo que de la editorial me informen que debo alargar la nota) pasa por la ciencia.
Si no me creen, por favor, dejen por un momento de lado vuestros microscopios y acérquense a la macroscópica mediática. Verán entonces que políticos, periodistas, economistas, jueces, empresarios y hasta avatares inexistentes hacen gala de una ignorancia supina pero no por ello menos rimbombante de disciplinas científicas como lo son la biología, la microbiología, la epidemiología y varias logías más.
Por favor, comprueben, certifiquen y reaseguren con vuestros propios ojos, oídos e incluso narices lo que estoy, desde mi propia ignorancia, afirmando. Y si los que no saben absolutamente nada saben (o hacen como si supieran) tanto, no quiero ni pensar lo que deben saber los que sí se han preparado durante años para la situación.
Llamativamente, estos son mucho más cautos que los ignorantes y suelen hablar (y más que afirmar categóricamente, proponer humildemente) solamente cuando son convocados a tal efecto.
Si me permiten, a todos aquelles que no parecen saber nada sobre la ciencia pero sí sobre ‘como parecer científico sin serlo’ les concederé el gracioso nombre de ‘cientificólogos/as’, reservándome el de ‘científicos’ para quienes se limitan a ser, sin preocuparse demasiado por ‘parecer’.
El problema de los cientificólogos es que primero hablan, afirman, concluyen, y recién después escuchan a quienes, consultados para confirmar lo dicho, no solamente no lo hacen, sino que lo ponen en duda, lo refutan y, peor aún, lo hacen con pruebas, datos, experiencia y documentos que podrían poner en duda la brillante y certera ignorancia de sus co-legos.
Quizá si invirtieran el orden y escucharan antes de hablar, las cosas serían de otro modo. Pero, esto ya lo sabemos, las cosas nunca son de otro modo. Y los cientificólogos tienen mucho menos espacio en los laboratorios y en los hospitales, pero mucho más en los medios y en los poderes varios.
Entonces, contra toda prueba, nos pueden decir que la vacuna rusa (Sputnik) nos puede alterar el ADN, corriendo el riesgo de que varios genetistas fallezcan de risa al escuchar semejante pavada, y de miedo al percatarse de que hay gente que la cree cierta. También pueden alertarnos de que la vacuna china puede provocarnos una tremenda propensión a comer arroz, y la cubana alterarnos el brazo izquierdo de manera que lo tengamos extendido hacia arriba y con el puño cerrado.
Todavía no se les ocurrió, pero no falta mucho para que nos digan que la vacuna inglesa nos cambiaría el habla y pondríamos los adjetivos antes de los sustantivos (¡una triste consecuencia, ¿no lo es?!), y que hablaríamos del clima día y noche. La japonesa nos haría sacar fotografías compulsivamente, como si fuéramos turistas en nuestra propia casa, o donde sea que cumplamos el aislamiento. La vacuna uruguaya nos volvería profundamente nostálgicos, la italiana nos convertiría en fogosos cineastas, la norteamericana nos llevarían a considerar de nuestra propiedad los departamentos de nuestros vecinos, y la suiza nos transformaría en seres voluptuosamente neutrales y apasionadamente puntuales.
Y por supuesto, habría una vacuna argentina. Mejor dicho, dos. Una más tranquila, con anticuerpos que primero duermen la siesta y después se ocupan del virus. La otra, ventajera, un tanto soberbia, que se autopercibe invencible, supone que el virus ‘conmigo no se va a meter’ y que sueña con triunfar en Europa.
Así estamos, queridos colegas.
Rudy
#TeRegaloUnTeorema
Mientras esperamos que el coronavirus afloje, #TeRegaloUnTeorema #TeRegalaUnModelo para intentar entender cómo se propaga una epidemia.
El proceso de contacto
En 1974, el gran TE Harris publicó el artículo ‘Contact interactions on a Lattice’ donde introdujo el hoy famoso ‘Proceso de contacto’
www.jstor.org/stable/pdf/2959099.pdf?refreqid=excelsior%3Add25654b7949ef4a31a90471c5a72e9f
Este proceso es un modelo estocástico con estructura espacial para la evolución de una epidemia. ‘Estructura espacial’ quiere decir que no solo nos importa cuántas personas están infectadas o sanas sino también dónde están localizadas. Es posiblemente el modelo más simple en donde aparecen una serie de fenómenos que uno desea que aparezcan al modelar este tipo de problemas.
¿Se lo puede complejizar? Sí. Un montón. Pero acá vamos con la versión más simple y es a propósito. Uno de los leitmotivs de la matemática es tratar de encontrar lo esencial. En lugar de buscar un modelo que tenga en cuenta todas las complejidades del caso, buscamos uno que sea lo más simple posible, pero que refleje las propiedades cualitativas de lo que queremos estudiar. En este caso, la epidemia.
El modelo es superfamoso porque además se convirtió en una herramienta muy potente para hacer matemática. Para estudiar modelos más complicados, para desarrollar ideas más complejas, etcétera. Es como un ladrillo fundamental que permite construir cosas mucho más elaboradas.
Dice así. Empezamos con una grilla. Piensen en un tablero de ajedrez gigante. Cada cuadradito representa un individuo que puede estar sano o infectado (como estamos buscando el modelo más simple posible, consideramos solo esas dos posibilidades). Los individuos no se mueven. Se quedan en su casillero para siempre. El estado de cada persona va cambiando a medida que pasa el tiempo. Puede pasar de sano a infectado o de infectado a sano. Cada uno de los que está infectado puede volverse sano a cierta ‘tasa’ que normalizaremos en 1. Por otra parte, cada individuo infectado puede infectar a cada uno de sus vecinos a cierta ‘tasa’ que llamaremos r . Es decir que un individuo sano se puede infectar a ‘tasa’ r x (cantidad de vecinos infectados).
Más preciso. Cada individuo (casillero), si está infectado, se va a recuperar en un tiempo aleatorio pero que, en promedio, vale 1. Si está sano, se va infectar en un tiempo aleatorio pero que, en promedio, es proporcional a la cantidad de vecinos infectados que tiene. La constante de proporcionalidad es r. Podemos pensar a r y a 1 como la velocidad a la que ocurren esas transiciones.
Aclaraciones: los vecinos de un individuo son los cuatro individuos que están arriba/abajo/izquierda/derecha. Los individuos no se mueven. Usamos varias veces la palabra ‘tasa’. La tasa a la que pasa algo significa que ese algo va a ocurrir en un tiempo aleatorio, ese tiempo es en promedio 1/tasa.
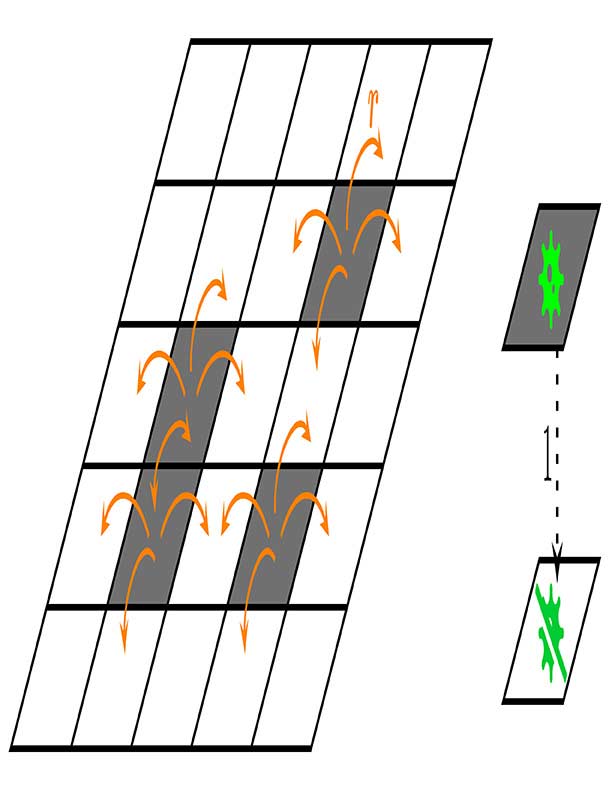
Si la tasa es grande, pasa rápido; si la tasa es chica, hay que esperar mucho para que pase. Si yo estoy sano y no tengo vecinos infectados, estoy tranca. Si tengo un vecino infectado, me voy a infectar a tasa r, si tengo dos, 2 × r; cuatro, 4 × r.
Harris demostró que si r es pequeño, la epidemia desaparece después de un tiempo. Pero si r es grande, hay probabilidad positiva de que la epidemia sobreviva para siempre y que el número de infectados crezca indefinidamente.
Da para pensar que la cuestión pasa por si r es mayor o menor que uno: r > 1 la epidemia se propaga, r < 1, la epidemia se extingue. Pero eso no es así debido a la estructura espacial que contempla el modelo. Y de hecho el valor crítico para r que divide aguas no se conoce. Se pueden obtener aproximaciones mediante simulaciones, pero nadie sabe calcularlo en forma exacta.
Para simulaciones, pueden ver una acá mate.dm.uba.ar/~leorolla/simulations/ y jugar con el tamaño de la grilla y el valor de r.
Después de Harris, miles de artículos se escribieron para entender cada vez más a este proceso, para usarlo para entender otros procesos y también para entender cómo se propagan las epidemias.
Nuestra humilde contribución: con Leo Rolla, Franco Arrejoría, Enrique Andjel y François Ezanno probamos dos propiedades del proceso de contacto. Pueden verlas acá projecteuclid.org/download/pdf_1/euclid.ejp/1465067138 y acá arxiv.org/pdf/1908.04175.pdf. En una próxima edición de #TeRegaloUnTeorema les cuento de qué se trata.
#TeRegaloUnTeorema
Robando rondas

Supongamos que tenemos un juego Arcade, de los denominados ‘fichines’, al que quieren jugar Ana, Beto, Cami y Dani.
Ana llega a las 19.00 y quiere jugar 30’
Beto llega a las 19.15 y quiere jugar 30’
Cami llega a las 19.30 y quiere jugar 15’
Dani llega a las 20.00 y quiere jugar 15’
Una forma de ordenarse sería la directa: se ponen en fila y cada persona juega, a su turno, el tiempo completo que quiere jugar y luego deja a la siguiente. Imaginémonos entonces a Ana jugando sus minutos, luego llega Beto, espera a que Ana termine y se pone a jugar, y en ese momento llega Cami que espera a que termine Beto, y cuando le toca a Cami a las 20.00 llega justo Dani, que la espera terminar para jugar. De esa manera, la ultima persona termina de jugar a las 20.30.
Pero…
¿Qué pasaría si el juego se jugara de a turnos de 15 minutos? (siempre privilegiando a quien todavía no haya jugado).
De esa forma, cuando llega Beto a las 19.15, ahí Ana debería dejarlo jugar a él sus primeros 15 minutos.
Con este nuevo esquema:
¿Terminarán todos de jugar para las 20.30? ¿O será antes?
¿Quién terminaría primero de jugar en este nuevo esquema?
¿Quién terminaría último de jugar?
¿Y qué sucedería si el turno es de 5 minutos? ¿Y de 1 minuto?
Corolario
Entre las tareas más importantes del sistema operativo de una computadora (por ejemplo, Linux o Windows) está la que se denomina planificación de procesos. Básicamente el sistema operativo tiene un problema interesante: ¿cómo hago para ejecutar cuatro programas a la vez en mi procesador (mi máquina Arcade)? Podemos pensar que Ana es el navegador de internet, Beto el procesador de texto, Cami el reproductor de video y Dani la calculadora, todos programas que compiten por el uso del procesador para poderse ejecutar.
La segunda estrategia, jugar por turnos, se denomina round robin (que no es un Robin redondo, sino más bien un ‘robo por rondas’), donde cada proceso va ‘robando’ un poquito de tiempo de procesador, y esto sucede muchísimas veces por segundo, lo que produce la ilusión de que hay varios programas ejecutándose a la vez, cuando en realidad es uno solo.
¿Puede una imagen estática percibirse con movimiento?
Mirá al centro de la imagen, donde se encuentra el círculo. ¿Percibís movimiento en la vista periférica? ¿Hacia dónde? ¿Es esto posible?

En los años 60 surgió dentro del arte contemporáneo el arte óptico (op art), cuyo propósito consistía en crear la ilusión de movimiento por medio de imágenes estáticas. Esto sirvió de base para que varios científicos cognitivos estudiaran este fenómeno; dentro de los cuales se destacó el doctor Akiyoshi Kitaoka, psicólogo cognitivo de la Universidad de Tokio, quien ha desarrollado muchas ilusiones de movimiento, incluidas sus famosas ‘serpientes giratorias’.
¿Por qué percibimos movimiento en una imagen estática?
Sabemos que existen neuronas complejas en las cortezas visuales que detectan movimiento. En realidad, solo detectan cambios de contrastes en una secuencia temporal. Si observan los pequeños rectángulos que forman la imagen, verán que tienen una secuencia de colores: negro, azul, blanco… embebido en un fondo amarillo. Pequeños movimientos de la retina (llamados microsacadas), que se realizan para escanear la imagen, hacen que estas neuronas complejas se ‘confundan’ y detecten estos cambios de contraste como movimiento. Si prestan atención a lo que experimentan, la sensación de movimiento se incrementa en la vista periférica. ¿Por qué? A medida que nos alejamos de la fóvea (el punto de la retina con el que hacemos foco y donde tenemos muchos conos, fotorreceptores responsables de la visión en color) hacia la periferia, disminuye la densidad de receptores visuales, de manera que la resolución de la imagen disminuye. Otra forma de decir esto es que finalmente cada neurona va a integrar la información de una mayor superficie del campo visual. Por ende, las neuronas complejas que incorporan información de la vista periférica son menos precisas y tienden a activarse más por estos cambios de contrastes de los rectángulos.
La imagen fue obtenida de Conway BR et al., ‘Neural basis for a powerful static motion illusion’, The Journal of Neuroscience, 25 (23): 5651-5656.
La dimensión desconocida
¿Cree usted en los rectángulos? ¿Alguna vez se encontró con uno en la vida real? Si su respuesta fue sí, entonces no tendrá problemas en creer en la existencia de los objetos de los que hablaremos a continuación: los fractales. Al igual que los rectángulos o los segmentos, estos son objetos matemáticos, y lo que vemos en la vida real son aproximaciones a ellos.
Una hoja de papel, por más fina que sea, no es un rectángulo. Un rectángulo, como objeto matemático, no tiene espesor. Así, si ‘apilamos’ muchos rectángulos el resultado no tendrá altura. Sin embargo, si apilamos muchas hojas de papel, como en el caso de una resma, el resultado tendrá cierta altura que dependerá de la cantidad de hojas utilizadas y su grosor. Algo similar ocurre con los segmentos: un trozo de hilo puede considerarse un segmento pero, si enrollamos mucho hilo, el resultado será como una pelota por lo que ocupará volumen en el espacio. Esto sucede porque todo en la vida real tiene tres dimensiones, a diferencia de un rectángulo verdadero que es bidimensional, o un segmento que es unidimensional. La hoja se considera un rectángulo cuando su espesor no importa, y un hilo se considera un segmento cuando solo nos interesa su longitud, pero no lo son. Lo mismo ocurre con los fractales: ciertas cosas en la naturaleza pueden considerarse fractales, aunque seguramente no lo sean.
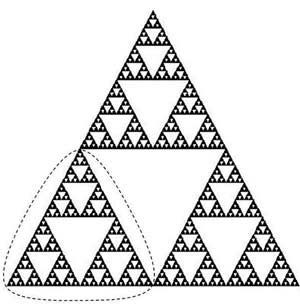
Vamos a presentar un caso particular de fractales: los autosemejantes o con autosimilitud exacta. Estos son aquellos donde el total contiene una cantidad finita de copias de sí mismo a menor escala, sin ningún tipo de distorsión. Luego, si hacemos zoom para observar el objeto con mayor detalle, cualquiera sea el grado de precisión elegido, nos encontramos con el mismo patrón que rige el todo. En la vida real, por supuesto, esta autosimilitud es limitada, ya que desaparece a cierto nivel de ampliación, como el es caso del romanesco:

Como dijimos antes, los fractales son objetos matemáticos. Una forma de construir fractales autosemejantes es mediante un algoritmo recursivo, es decir, una instrucción que se repite infinitas veces. Por ejemplo, el triángulo de Sierpinski se construye de forma recursiva como sigue:
Dibujar un triángulo equilátero.
Marcar el punto medio de cada lado y conectarlos. Quedan así 4 triángulos.
Eliminar el triángulo central y repetir el proceso en cada uno de los que quedan, infinitas veces.

¿Podemos determinar la dimensión del triángulo de Sierpinski? Existen distintas dimensiones que se usan en geometría fractal, pero vamos a considerar la dimensión de homotecia. Aunque no daremos una definición formal, la ilustraremos en el caso de nuestro triángulo. Para ello, veamos por qué decimos que un segmento tiene dimensión 1, que un cuadrado tiene dimensión 2, o que un cubo dimensión 3. Lo haremos de una manera poco formal en el sentido matemático, para ilustrar la idea.
Supongamos que llevo a una fotocopiadora una hoja con un segmento dibujado en ella y pido que me la amplíen, digamos al doble. ¿Cuántos segmentos como el original necesito para cubrir la imagen ampliada? Claramente, serán 2=21. Pensemos ahora qué ocurre si en lugar de un segmento llevo un cuadrado. ¿Cuántos cuadrados como el original necesito para cubrir la imagen ampliada? Ahora serán 4=22. Si pudiéramos hacer lo mismo con un cubo, digamos en una impresora 3D, cuántos cubos de lado l necesito para cubrir uno de lado 2l? En este caso necesito 8=23. Estos exponentes son, precisamente, las dimensiones de estos objetos, respectivamente.
Así, la dimensión de homotecia d de un objeto autosemajente es el exponente que satisface N=Zd, siendo N la cantidad de copias del objeto necesarias para cubrir el objeto ‘ampliado por Z’, en el sentido de arriba.
Con esta definición, ¿cuál es la dimensión del triángulo de Sierpinski?
Soluciones
Robando rondas
El horario en que todxs terminaron de jugar es el mismo: las 20.30; acá termina primero Cami (porque a las 19.45 cuando llega la dejan jugar, y juega su turno entero), y quien terminaría último de jugar sería Beto, porque luego de dejar jugar a Dani termina Ana, y recién después termina Beto. Al bajar el tiempo del turno, lo que empieza a pasar es que, cuando llega Beto, él y Ana se empiezan a turnar hasta que llega Cami y se empiezan a turnar entre los 3, y ahí sí va terminando primero Ana nuevamente.
La dimensión desconocida
Si duplicamos el tamaño del triángulo de Sierpinski necesitaremos 3 copias del original para cubrirlo. Así, su dimensión d es el número que satisface 3 = 2d Luego, este objeto tiene dimensión igual a log3/log2, que resulta un número no entero comprendido entre 1 y 2.
Equipo de la sección ‘Matemática, ilusiones y humor’
Marilina Carena
Matemática, UNL-Conicet.
[email protected]
Nicolás Fernández Larrosa
Biólogo, IFIBYNE, UBA-Conicet.
[email protected]
Pablo Groisman
Matemático, UBA-Conicet.
[email protected]
Juan Pablo Pinasco
Matemático, UBA-Conicet.
[email protected]
Nicolás Pírez (coordinador)
Neurobiólogo, IFIBYNE, UBA-Conicet.
[email protected]
Rudy
Humorista.
[email protected]
Alfredo Sanzo
Ingeniero, ICC, UBA-Conicet.
[email protected]
Nicolás Sirolli
Matemático, UBA-Conicet.
[email protected]
Preguntas, comentarios y sugerencias: [email protected]











