Caramelos por toda la plata
En el número anterior dejamos pendiente el problema de determinar el resultado de dividir cero entre cero. Vimos que si dividimos cualquier número no nulo por cero se obtiene como resultado infinito, que no es un número, sino que es un símbolo que denota un valor tan grande como se quiera. Para ver esto fuimos haciendo cada vez más chico el divisor para ‘acercarnos’ al cero.
Entonces podemos aplicar el mismo razonamiento para determinar el resultado de ‘cero dividido cero’. Ahora tenemos dos ceros a los que acercarnos: el dividendo y el divisor. Para no usar estos términos específicos, volvamos al ejemplo de los caramelos.
La situación era la siguiente: voy a un kiosco con 100 pesos y quiero saber cuántos caramelos puedo comprar, según el precio unitario. La respuesta es simple:
Caramelos que puedo comprar =
dinero que llevo ÷ precio unitario
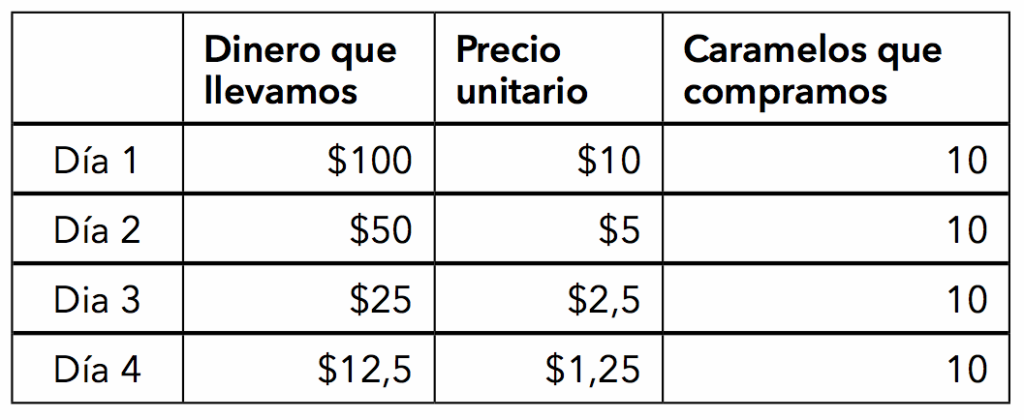
Para saber el resultado de dividir por cero fuimos achicando el precio unitario cada vez más. Es decir, los caramelos eran cada vez más baratos. Pero ahora, además, llevaremos cada vez menos plata para así acercarnos al ‘otro cero’ involucrado. Así, supongamos que el primer día vamos al kiosco con 100 pesos y que cada caramelo cuesta 10 pesos. Cada día que pasa el kiosquero baja el precio a la mitad y nosotros llevamos, también, la mitad de dinero que el día anterior. ¿Cuántos caramelos compramos cada día? Pongamos la información en una tabla para organizarnos:
¿De qué color es el gato?
Quizá percibas que el gato es verde (A) o violeta (B), pero en ambos casos es blanco y gris (C). ¿Por qué ocurre que lo percibimos de diferentes colores? Esta ilusión, conocida como ilusión de Munker, muestra hasta qué punto la percepción del color está influida por el contexto. A diferencia de otras ilusiones de contraste (ver por ejemplo ‘Crossfit cerebral N.º 5’, Ciencia Hoy, 172), aquí el color con el que se percibe el gato depende principalmente del color de encuadre del primer plano (las rayas que cruzan la imagen del gato), mientras el efecto de la ilusión se vuelve más fuerte si el color del fondo es un opuesto. De esta manera, a pesar de que la imagen del gato es monocromática, a nivel de nuestra corteza visual se asimila el color predominante, induciéndose un relleno visual de color.

Los juegos del Pleistoceno
El 7 de marzo de este año se publicó ‘Ice Age megafauna rock art in the Colombian Amazon?’, de José Iriarte, Michael Ziegler, Alan Outram, Mark Robinson, Patrick Roberts, Francisco Aceituno, Gaspar Morcote-Ríos y Michael Keesey, en Philosophical Transactions of the Royal Society.
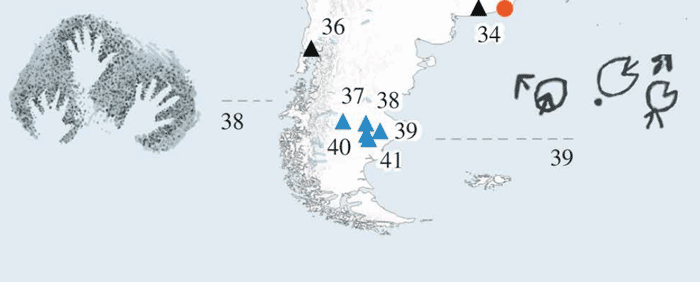
Si bien el propósito del artículo apunta al problema de identificar megafauna ya extinguida que se distingue en los dibujos, la figura 1 del artículo nos deja pensando también en los juegos y entretenimientos de la early human history of South America (por citar la última frase de la introducción, que no necesita mayor traducción).
Observamos, en un recorte de la figura, que antes de la invención de la tijera, la estrategia dominante era jugar ‘papel’ contra la opción ‘piedra’, como lo documentan los registros de la Cueva de las Manos.
Vemos también, en Piedra Museo, la astucia de jugar al Pac-Man antes de la invención de las calles, indicando con un vector la dirección y el sentido del movimiento.
¡Quién sabe qué otros juegos de la época habrán quedado documentados!
¿Palabras o programas?
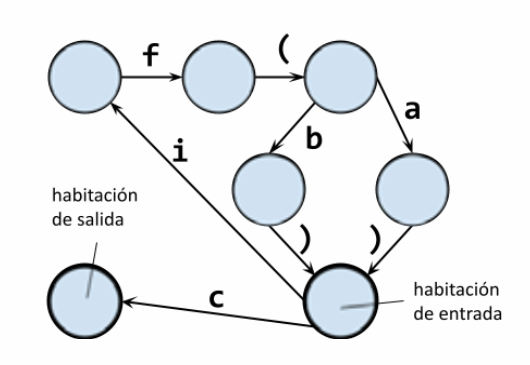
Estás en una sala de escape en la entrada, y tenés una palabra en la mano. La forma de salir es utilizar las letras de la palabra para ir pasando de habitación en habitación. A medida que vas leyendo una letra, vas pasando a la habitación indicada por la flecha correspondiente. ¿Podés llegar a la habitación de salida leyendo las siguientes palabras? ¿Cuáles son las reglas generales para una palabra ‘aceptada’?
1) if (a) c
2) c
3) if (if (a)) c
4) if (b) if(a) c
5) if (a) if(b) if (a)
6) if (a) if(b) if c)
7) if (a) if(b) if (a) c
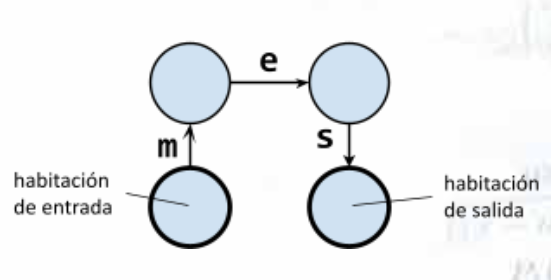
Por ejemplo, en la siguiente sala de escape, con la palabra ‘mes’ puedo llegar hasta la habitación de salida, pero con la palabra ‘mermelada’ no puedo llegar a ningún lado.
Corolario
Los programas de computadora se suelen escribir como un texto muy riguroso y esquemático, que debe respetar las reglas de un lenguaje. ¿Cómo sabemos si un texto escrito respeta las reglas del lenguaje?
Utilizando un ‘mapa de habitaciones’ similar a este, que se conoce como autómata.
#TeRegaloUnTeorema
Teorema
Entre todas las figuras planas de perímetro dado L, la que tiene mayor área es el círculo.
Es decir, si nos dan un alambre y nos piden que le demos forma para encerrar la mayor cantidad de área posible, conviene hacer una circunferencia.
Se lo llama también problema de Dido, fundadora y primera reina de la ciudad fenicia de Cartago, en Túnez. Según la leyenda, Dido llegó al actual golfo de Túnez allá por el siglo VIII antes de nuestra era y pidió que le den tanta tierra como la que se pueda encerrar con la piel de un toro. Aceptado el pedido, cortó la piel de un toro en largas y finas tiras y con ellas encerró la mayor superficie posible: la ciudad de Cartago.
El problema de Dido es en realidad un poco distinto –pero muy relacionado–, porque la ciudad de Cartago se extendía sobre la costa del mar Mediterráneo y entonces la pregunta de Dido era cuál es la figura que debemos construir para obtener la mayor cantidad de área posible con un arco que va desde un punto de la costa hasta otro. La respuesta es que lo mejor es hacer un semicírculo.
Así de viejo es el problema, y ya en la antigua Grecia sabían que la respuesta era el círculo, gracias a un tal Zenodoro, pero su demostración llegó recién a mediados del siglo XIX gracias a Jakob Steiner, que en el camino inventó un método que dio lugar a toda una estrategia para resolver muchísimos problemas. Hoy lo llamamos simetrización de Steiner y es una herramienta fundamental en lo que se denomina análisis geométrico.

Pero… pará, pará pará. La demostración de Steiner tampoco estaba del todo bien, al menos para los parámetros actuales. Steiner demostró que si había una solución al problema tenía que ser un círculo, mostrando justamente que una figura óptima debía ser tan simétrica que solo un círculo podría lograrlo.
Pero le faltó demostrar que existía una solución al problema. Hoy sabemos muy bien que podría pasar (no es lo que pasa, pero una demostración que se precie debe contemplar mostrar que efectivamente no pasa) que haya una sucesión de figuras planas que van teniendo cada vez más y más área pero que no haya ninguna que sea la que mayor área tiene.
De hecho eso es lo que pasa si nos preguntamos por la figura que debemos construir para encerrar la menor área posible. Los invito a pensar cómo podrían construir figuras bidimensionales con área tan chica como quieran, todas con el mismo perímetro. Pero resulta que no hay ninguna que sea la que tiene el área más chica posible.
En el camino, antes de que Steiner nos regalara su hermosa prueba, pasó lo que suele pasar con los grandes problemas. Tal vez sea exactamente eso lo que los hace grandes. El intento de demostración de la desigualdad isoperimétrica motivó el desarrollo del cálculo de variaciones, un área fundamental de la matemática actual para resolver problemas intrínsecos de la matemática pero también de física, ingeniería, economía y muchas más. ¿Los protagonistas? Un tal Leonard Euler, los hermanos Johann y Jakob Bernoulli y el joven Joseph-Louis Lagrange con sus diecinueve añitos.
El cálculo de variaciones vino como corolario obligado del desarrollo del cálculo infinitesimal por Leibniz y Newton, y llegó para cambiar nuestras vidas para siempre. Me animo a decir que nuestro mundo no sería ni por asomo como lo conocemos sin él. No soy el único.
Esencialmente trata de resolver problemas de encontrar máximos y mínimos de ciertas funciones como los que muchos conocen de un primer curso de cálculo pero en donde las variables son objetos más generales: curvas, funciones, superficies, conjuntos, etcétera.
La desigualdad isoperimétrica tiene también versión 3D (y 4D, 5D, etcétera) que dice que si queremos encerrar mucho volumen con una sábana, lo mejor es hacer una pelota. O al revés, si queremos encerrar un volumen fijo, usando la menor cantidad posible de globo, lo mejor es hacerlo redondo.
Por eso las gotas de lluvia y las pompas de jabón son redondas. La naturaleza es sabia. O no sé si sabia, pero al menos la tensión superficial (las moléculas en el borde de la gota ‘quieren’ juntarse) lleva a que se minimice el área de la superficie que las encierra. Y la única forma de que eso pase, de acuerdo con este teorema, es tomando forma redonda.
Ver video: upload.wikimedia.org/wikipedia/commons/f/f8/Cutting_a_water_droplet_using_a_superhydrophobic_knife_on_superhydrophobic_surfaces.ogv
Además de la versión 3D, la desigualdad isoperimétrica se ha extendido a muchos otros contextos: esferas, superficies más complicadas, grafos y otros espacios más abstractos aún. Se ha vuelto una herramienta indispensable para estudiar muchos fenómenos, por ejemplo, el comportamiento de un caminante aleatorio, que sirve a la vez para modelar innumerables situaciones en física, biología, finanzas y mucho más.
#TeRegaloUnTeorema
Soluciones
Caramelos por toda la plata
En el primer caso la cantidad de caramelos que podemos comprar cada día aumenta, siendo el doble del día anterior (se dice que ‘tiende a infinito’). En el segundo caso disminuye, y cada día podremos comprar la mitad que el día anterior (‘tiende a cero’, suponiendo que los caramelos se pueden fraccionar todo lo que se quiera).
¿Palabras o programas?
Las palabras (o programas) que nuestro autómata reconoce son el 1, el 2, el 4 y el 7. Los únicos programas válidos son aquellos que dicen if (a) o if (b) y luego seguidos por cuantos if (a) o if (b) se quiera, pero siempre terminando en c.
Marilina Carena
Matemática, UNL-Conicet.
[email protected]
Nicolás Fernández Larrosa
Biólogo, IFIBYNE, UBA-Conicet.
[email protected]
Pablo Groisman
Matemático, UBA-Conicet.
[email protected]
Matías López-Rosenfeld
Computador, UBA-Conicet
[email protected]
Juan Pablo Pinasco
Matemático, UBA-Conicet.
[email protected]
Nicolás Pírez (coordinador)
Neurobiólogo, IFIBYNE, UBA-Conicet.
[email protected]
Alfredo Sanzo
Ingeniero, ICC, UBA-Conicet.
[email protected]
Nicolás Sirolli
Matemático, UBA-Conicet.
[email protected]











