Demoliendo reglas
Si planteo la siguiente secuencia numérica:
2, 4, 8, 16, …
y luego pregunto qué número cree usted que continúa, es muy probable que la respuesta sea 32. Y esto tiene sentido porque en nuestra mente determinamos una regla que están cumpliendo los números dados: cada uno que aparece es el doble del anterior. Pero ¿es esta la única regla que cumplen? ¿No habrá otra regla a la que se ajusten estos números y, por lo tanto, haya otro posible candidato para ser el siguiente? Más aún, dado cualquier candidato para ocupar la quinta posición, ¿habrá una regla a la que se ajusten todos los números de la nueva lista?
Lo anterior tiene que ver con la paradoja de Wittgenstein, la cual enuncia que una regla no puede determinar ningún curso de acción porque todo curso de acción puede hacerse concordar con la regla.
Si bien de esto se puede desprender un amplio debate filosófico, solamente me atrevo a hablar sobre su relación con una lista finita de números como la del inicio. Esto es algo que sabe explicar muy bien el escritor y matemático Guillermo Martínez, autor de Crímenes imperceptibles, entre otras obras. Guillermo se refirió a este tema en varias charlas y entrevistas sobre series lógicas y crímenes en serie, y voy a tomar algunas de sus ideas como punto de partida para responder las preguntas hechas al principio. Creo que, de hecho, todas se responden si logramos comprender que no importa cuántos ejemplos nos muestren de una regla, no podemos inferir la regla a partir de ellos o, en otras palabras, ninguna lista finita de números tiene, en general, una continuación única.
Para entender esto vamos a suponer que la regla que nos quieren hacer pensar es la del comienzo: cada número es el doble del anterior, y que para ello nos muestran los 3 primeros números de la lista. A saber:
2, 4, 8, …
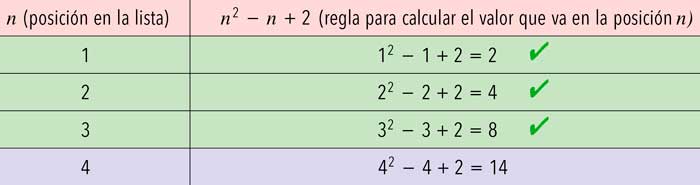
¿Alcanza esto para determinar la regla? La regla que queremos se puede traducir simbólicamente como que en la posiciónnde la lista se encuentra el número 2n, es decir, en el primer lugar está el 2, en el segundo lugar está 22, en el tercero aparece 23, y así. Según esta regla, en la cuarta posición corresponde el número 24 = 16. Sin embargo es sencillo de verificar que los tres números dados también cumplen, por ejemplo, la siguiente instrucción: en la posición n se encuentra el número n2 – n + 2. Para verificarlo y, a su vez, determinar quién sigue, organicemos la información en una tabla:
Así, según esta regla, el candidato para ocupar el cuarto puesto de la lista es el número 14.
Podríamos entonces pensar que la información que teníamos era muy poca como para poder determinar la regla y que, tal vez, esta sí queda definida si conocemos un número más. Así, supongamos que el dato es el siguiente:
2, 4, 8, 16, …
Se puede ver que los datos en esta lista se ajustan ahora a la regla (n3 – 3n2 + 8n)/3, donde n indica, como antes, la posición. Según esto, ¿qué número ocuparía el quinto lugar en la lista?
Esto va a seguir pasando siempre: por más que la lista se haga más larga, vamos a poder encontrar una regla que se ajuste a ella que no sea, necesariamente, la que esperamos. Es claro que la regla se va haciendo cada vez menos ‘natural’, pero tampoco existe un criterio que mida esta naturalidad como para poder establecer cuál es la más indicada. Esto implica que cualquier otro número podría ser el siguiente, ya que dada cualquier lista finita de números podemos encontrar una regla que se ajuste a ellos. Una forma de encontrar dicha regla es mediante teoremas de interpolación (ampliaremos esto en el próximo número). Pero existen muchos caminos para encontrar una regla. Por ejemplo, mediante un enfoque geométrico, como muestra Guillermo Martínez (mirá el ejemplo escaneando el codigo QR), lo que deja de lado cualquier criterio sobre lo elegante, lo fácil o lo ‘natural’, como pretendíamos antes.
Conclusión: cuando alguien nos presente una lista finita de números y pregunte cuál es el siguiente, la respuesta es que ¡cualquiera puede serlo! Y si no logra convencerlo con todo lo anterior, en el próximo número veremos cómo construir una regla que compruebe esto.
¿Me reconocééééééés?
Volvemos al caso de la sala de escape que vimos en el número anterior, nuestro autómata. Recordemos que la forma de transitar por la sala es, dada una palabra que tenés en la mano, ir utilizando las letras para pasar de habitación en habitación a medida que vas leyendo una letra y transitando por la flecha correspondiente.
Recordemos un ejemplo:
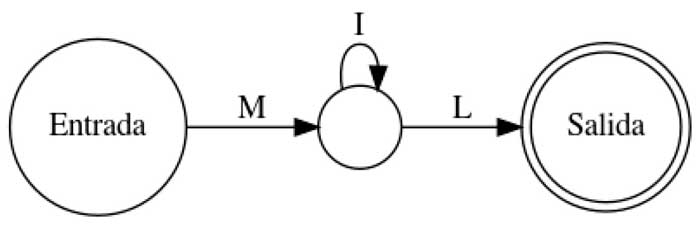
Se puede salir de la sala teniendo en la mano la palabra ML, MIL, MIIL, MIIIIL, MIII… IIL, pero no con MI, ni MIII, ni ninguna otra cosa que no sea M, ninguna o algunas I y una L. Se dice entonces que nuestro autómata reconoce todas las palabras que comienzan con M y terminan con L, y con varias I entre ellas, e incluso sin ninguna.
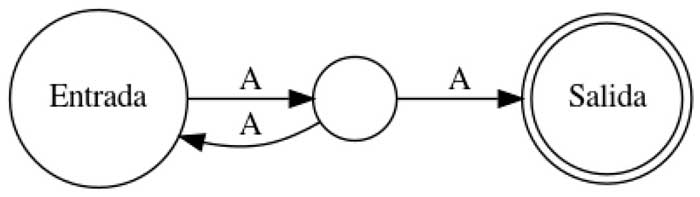
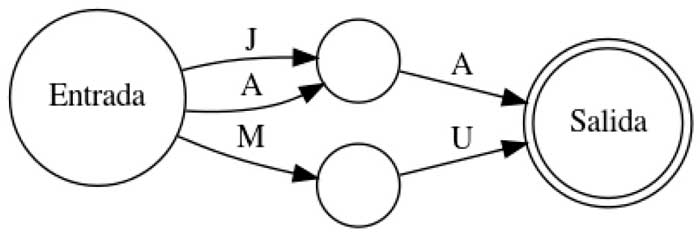
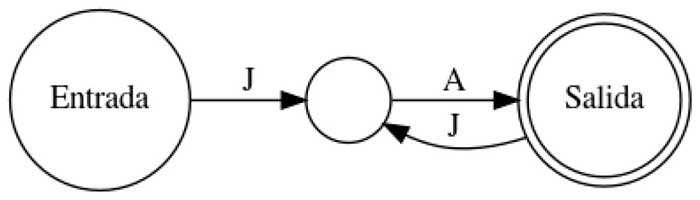
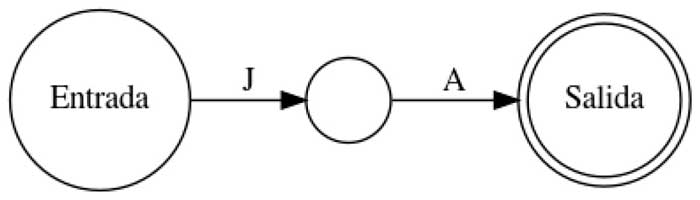
El objetivo de hoy es decir a qué autómata corresponde cada descripción:
A. Reconoce únicamente la palabra JA.
B. Reconoce las palabras JA y AA (y alguna más, ¿cuál?).
C. Reconoce las palabras que son risas: JA, JAJA, JA JA JA… y así.
D. Reconoce las palabras que tienen únicamente y exactamente una cantidad par de letras A: AA, AAAA, AAAAAA, …
Conclusión
X-le
Si me preguntan quién se lleva el Nobel en la categoría ‘Juegos de ingenio’ del año 2022, no tengo dudas: el wordle. Dudé en otorgarle el Oscar también, pero quiero evitarme una cachetada por algún mal chiste.
¿Es nuevo este juego? Mmmm nnnnoo creo… en los 80 jugaba con mi hermano a una versión numérica, para dos jugadores:
A y B eligen cada uno un número de 4 cifras en secreto;
A le dice a B un número, y B le responde cuántos dígitos están bien ubicados y cuántos figuran en el número pero no están bien ubicados;
B le dice a A un número, y A…
Se alternan, y gana el que descubre el número del otro (si es A, B puede tener otra oportunidad, y empatan si también lo descubre).
Federico, mi hijo, se ha hecho fanático del wordle y su variantes. Antes de ir a la escuela (y/o a la vuelta) juega media docena de X-le, donde X se reemplaza por word (en español, a veces con tildes, pocas en inglés), bolud (con palabras típicamente argentas), world (dan un mapa, uno sugiere países, la ayuda es en qué dirección –N, NE, E…– queda el correcto, y qué distancia hay entre las capitales). Y juega otros matemáticos: nerd, oood, summ… Estas variantes las encontró en la página https://gamovil.com, hay para series, películas, música… pero no está mi favorito: el chessle. Si lo juegan, les dejo una pista: traduzcan la notación algebraica moderna (1. e4 c5, 2. Cf3 Cc6…) a la vieja (1. P4R P4AD, 2. C3AR C3AD…), me lo van a agradecer.
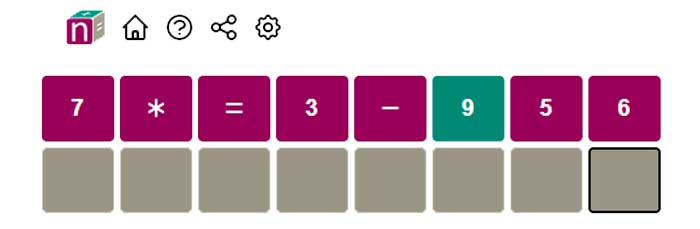
Para ir terminando, el muy recomendable nerdle tiene además distintas opciones (www.nerdlegame.com). Una de ellas, instant nerdle, se presta para plantear acá porque no se necesita feedback: nos dan una lista de dígitos y símbolos matemáticos, y debemos reordenarlos para que se cumpla una igualdad. Los de color verde están bien ubicados; los púrpura, no. Les dejo una captura como ejemplo, y la respuesta está en las soluciones. Mejor dicho, están, porque este tiene dos soluciones:
Demoliendo reglas
Según la regla dada, el número siguiente en la lista es 30.
¿Me reconocééééééés?
A-4, B-2 (y reconoce MU también), C-3, D-1
X-le
El problema tiene dos soluciones, la oficial es 57 – 6 * 9 = 3. Y la alternativa, haciendo pasaje de términos, 57 – 3 = 9 * 6. Según las reglas, esta otra no es válida porque no debe haber operaciones después del igual.
Marilina Carena
Matemática, UNL-Conicet.
[email protected]
Nicolás Fernández Larrosa
Biólogo, IFIBYNE, UBA-Conicet.
[email protected]
Pablo Groisman
Matemático, UBA-Conicet.
[email protected]
Matías López-Rosenfeld
Computador, UBA-Conicet
[email protected]
Mariano I Martinez (coordinador)
Biólogo, MACN-Conicet
[email protected]
Juan Pablo Pinasco
Matemático, UBA-Conicet.
[email protected]
Nicolás Pírez (coordinador)
Neurobiólogo, IFIBYNE, UBA-Conicet.
[email protected]
Alfredo Sanzo
Ingeniero, ICC, UBA-Conicet.
[email protected]











