Rudy:
Tus compañeros y compañera de Crossfit Cerebral queremos agradecerte por haber compartido con nosotros esta sección desde sus inicios. ¡Gracias por hacer que la ciencia nos resulte (aún) más divertida! Te despedimos (solamente de esta sección) cálidamente.
Cero lógica
Desde que comenzó la pandemia varios conceptos matemáticos empezaron a sonar en los medios de comunicación: exponencial (por el contagio), estadísticas, análisis de gráficos, curvas (que debíamos aplanar), porcentajes (por la efectividad de las vacunas)… Pero hubo un concepto cuyo debate resultó, de hecho, algo divertido: la paridad del 0. Todo se originó con un anuncio que establecía qué días podían circular las personas, según si su DNI era par o impar.
Fue así que la medida se anunció, hace poco más de un año, de esta manera: las personas cuyos documentos terminen en un dígito par podrán salir determinados días; los que terminen en impar, los restantes.
La intención fue simplificar el anuncio evitando que alguien deba preguntarse si un número que supera los 10 millones es par o impar, utilizando este criterio equivalente. Sin embargo, lejos de eso, fue ahí cuando arrancó el problema. Automáticamente las redes se llenaron de la misma pregunta: ¿y los que terminan en 0 cuándo salen? Los medios rápidamente se hicieron eco de esto. Es que para muchas personas el 0 no es nada, ni par ni impar.
Antes que nada dejemos en claro que el 0 es un número par, y no hay ninguna duda sobre ello. ¿Por qué? Sencillamente porque hay una definición de número par, y el 0 la cumple. Hay muchas formas equivalentes para definir cuándo un número es par, pero una posible es:
Si al dividir un número x por 2 se obtiene resto igual a 0, entonces x es un número par. (*)
Si dividimos 7 entre 2, el cociente es 3 y el resto 1. Entonces 7 no es par. En cambio, si dividimos 8 entre 2, el cociente es 4 y resto 0, por lo que 8 es par. De la misma forma, si dividimos 0 entre 2, tanto el cociente como el resto son iguales a 0, así que el 0 es par. Sin embargo, no vayan a apostar por el cero como par en la ruleta. En la ruleta no se entrega premio cuando uno apuesta por pares y sale el cero. Esto no tiene que ver con la paridad del 0, sino que está especificado en el reglamento y es para equilibrar las probabilidades entre pares e impares sobre los 36 números restantes.
En el caso particular del enunciado (*), también vale el recíproco:
Si x es un número par, entonces al dividir x entre 2 se obtiene resto igual a 0.
En otras palabras, los enunciados A y B siguientes son equivalentes:
A: El resto de dividir el número x entre 2 es igual a 0.
B: El número x es par.
¿Qué significa que sean equivalentes? Vayamos por partes. En matemática, si afirmamos que ‘A implica B’, significa que cuando A vale, entonces B también. Solamente esto. Por ejemplo, partamos del siguiente enunciado con relación a la COVID-19:
Si una persona tiene más de sesenta años, entonces es considerada de riesgo. (+)
En la afirmación anterior, tenemos:
A: Tener más de sesenta años.
B: Ser de riesgo.
La afirmación dada es verdadera en cuanto a considerar a una persona dentro del grupo de riesgo: si A, entonces B. En otras palabras, A implica B. ¿Se puede deducir de esto alguna de las siguientes afirmaciones?
1. Si es de riesgo, entonces tiene más de sesenta años.’
2. Si no tiene más de sesenta años, entonces no es de riesgo.’
3. Si no es de riesgo, entonces no tiene más de sesenta años.’
Claramente 1 y 2 son conclusiones incorrectas: una persona puede ser de riesgo por tener alguna enfermedad aunque sea joven. Esto, que se ve tan claro con este ejemplo concreto, suele traer problemas cuando se trabaja con proposiciones en matemática, en donde la cosa se pone más abstracta. La afirmación 1) corresponde al recíproco de (+), es decir, ‘B implica A’. Lo establecido en 2) es ‘no A implica no B’, es decir, suponer que porque no vale la hipótesis en (+), entonces necesariamente no vale la conclusión. Como vemos, ninguna de estas deducciones pueden obtenerse de la afirmación hecha en (+).
La afirmación que sí es cierta es la establecida en 3) ya que, si una persona tuviera más de sesenta años, entonces sería de riesgo. Como no lo es, no tiene más de sesenta años. Esto se llama contrarrecíproco de (+): ‘no B implica no A’, y se deduce de la veracidad de (+).
Volviendo a la paridad del 0, mencionamos que los enunciados A y B dados al comienzo son equivalentes, lo que en matemática se expresa como ‘A si y solo si B’, y significa que A implica B y que, además, B implica A.
Aunque en matemática resulta muy importante utilizar las implicaciones de forma correcta para no llegar a conclusiones erróneas, también lo es en lo cotidiano. Es muy frecuente encontrar falacias lógicas en discursos: se utilizan argumentos que parecen válidos para atacar o invalidar otra opinión, pero no lo son. Esto puede ser intencional o, simplemente, por descuido o ignorancia. Para no ser víctimas de algunas de estas falacias dejamos algunas preguntas para entrenar nuestra lógica. Para esto, vamos a suponer que una persona cumple exactamente con lo que afirma (como si fuera un contrato). Esta persona afirma:
‘Si el examen comienza por la tarde, entonces iré caminando.’
¿Cuáles de las siguientes conclusiones pueden deducirse con certeza de la afirmación anterior?
1. Si fue caminando, entonces el examen comenzó por la tarde.
2. Si el examen comienza por la noche, entonces no irá caminando.
3. Si no fue caminando, entonces el examen no comenzó por la tarde.
#TeRegaloUnTeorema
Teorema de Euclides. Hay infinitos números primos.
Este teorema, que es una pieza fundamental de la matemática, fue probado por Euclides en uno de los trece libros que componen los Elementos, unos trescientos años antes de nuestra era.
Es increíble por donde se lo mire:
por la simpleza de su enunciado;
por su demostración simple, corta, conceptual, constructiva y (si querés ponerle onda) bella;
por lo fundamental que resulta el teorema, y
por lo que perdura.
Luego de Euclides, muchísimas nuevas pruebas se han dado sobre la infinitud de los números primos. Ninguna parece superar a la de Euclides.
Antes de empezar con la demostración, un breve repaso. Los números naturales son el 1, el 2, el 3…, etc. Un número natural es primo si solo es divisible por 1 y por él mismo. El número y es divisible por el número x quiere decir que cuando dividimos a y por x nos da un número entero (o que no hay resto). También a veces decimos que x divide a y. Si un número no es primo, decimos que es compuesto.
Ahora sí…
Demostración. Se toma un conjunto arbitrario pero finito de números primos
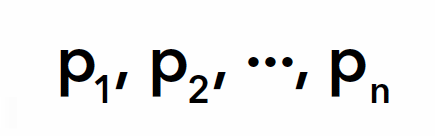
y se considera el producto de todos ellos más uno,
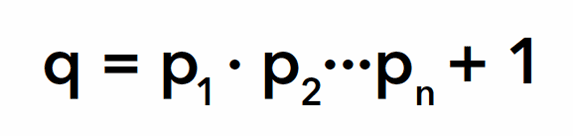
Este número es mayor que 1 y distinto de todos los primos de la lista.
El número q puede ser primo o compuesto. Si es primo tendremos un número primo que no está en el conjunto original. Si, por el contrario, es compuesto, entonces existirá algún factor p que divida a q.
Suponiendo que p es alguno de los primos de la lista se deduce entonces que p divide a la diferencia
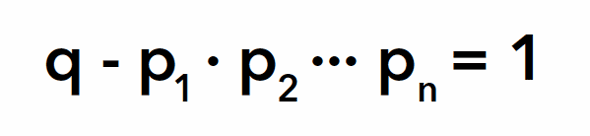
Pero ningún número primo puede dividir a 1, es decir que p no está en la lista. La consecuencia es que el conjunto que se escogió no es exhaustivo, ya que existen números primos que no pertenecen a él, y esto es independiente del conjunto finito que se tome. Podemos agregar a p a esta lista y volver a repetir el procedimiento. De esta forma vemos que siempre podemos agregar un número más a la lista de números primos y por lo tanto tiene que ser infinita.
#teregalounteorema
Mi gata tiene el poder hipnótico de desaparecer sus huellas…
Frina (mi gata) tiene el poder de hacer desaparecer sus huellas con solo mirarle los ojos fijamente durante varios segundos.

En realidad, a pesar de haber sido idolatrados por civilizaciones enteras, los gatos no tienen ese poder. Lo que ocurre es una ilusión óptica. Cuando fijamos la mirada en los ojos de Frina, esa parte del campo visual coincide con nuestra fóvea en la retina: la zona donde tenemos más receptores visuales y, por ende, mayor resolución de la imagen visual (es donde hacemos foco). A medida que nos alejamos de la fóvea (en la retina) disminuyen los receptores visuales y la imagen se vuelve menos definida. Aun así, podemos reconocer las huellas de Frina con nuestra visión periférica. Pero, entonces, ¿por qué desaparecen después de unos segundos? Al cabo de unos momentos, nuestra corteza visual (el área del cerebro que procesa la información visual), al no detectar cambios a nivel de nuestra visión periférica, filtra la información que considera irrelevante: entonces, las huellas de Frina desaparecen como parte del fondo. Este tipo de ceguera visual está regulada por nuestra atención (estamos prestando fuertemente la atención a los ojos de Frina) y es un ejemplo de modulación top-down: es decir, de áreas cognitivas (relacionadas con la atención) hacia áreas sensoriales (en este caso, visual).
La letra más usada
En el número anterior vimos un sistema para encriptar y desencriptar: el método del César. Este método consistía en reemplazar cada letra de un mensaje por otra, siempre desplazando una cantidad fija. Por ejemplo, si el desplazamiento era 1, la A se reemplaza por la B, la B por la C y así… hasta la Z por la A. Con desplazamiento 2, la A por la C… y así. Para desencriptar un mensaje alcanzaba con hacer la operación inversa. Pero… ¿qué pasaría si la forma de encriptar no fuera un alfabeto desplazado?
En la preparación de este número recibimos el siguiente mensaje enviado por lectores:

Este mensaje claramente ha sido encriptado (…a menos que hayan querido decir: ‘gato, león, mono, caballo, elefante’…).
En este caso no sabemos cómo ha sido encriptado el mensaje, entonces tendremos que ingeniarnos de alguna otra manera para descubrir cuál es el mensaje oculto por estos simpáticos animales.
Sabemos, sí, que el mensaje está escrito en castellano y es lo que vamos a usar fuertemente para poder trabajar. En nuestro idioma, las letras no aparecen todas con la misma frecuencia, por ejemplo, las vocales son más comunes que algunas consonantes (creo que estamos todos de acuerdo que es más común ver una e que una x o una w). Entonces, ¿qué pasaría si leyéramos montones y montones de textos en castellano y anotáramos para cada letra cuántas veces la vimos? Por ejemplo, si lo hacemos con el primer párrafo de este artículo (el que comienza por ‘En el número anterior…’) tendremos que:
la a aparece 66 veces;
la e aparece 46 veces;
… (así con el resto), y
la g, la k, la w y la x no aparecen nunca.
Es cierto que es un caso puntual de un párrafo que tomamos de ejemplo. Pero podemos repetir esto con muchísimos textos muy extensos y empezaremos a tener algo que es representativo del lenguaje. Nos hemos tomado el atrevimiento de hacer esta tarea y lo que se obtiene puede verse en el siguiente gráfico:
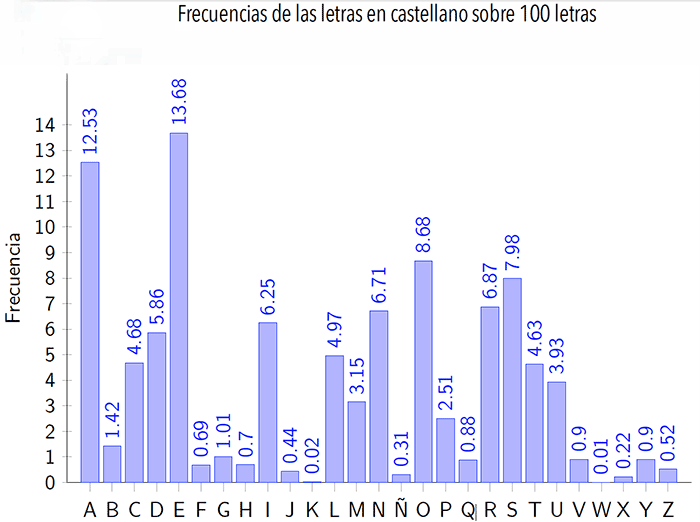
En este caso, en lugar de tener la cantidad de letras contadas, lo que hicimos fue expresarlo como proporción. Es decir, en lugar de escribir que tenemos 15.343.518.564.654 letras e, lo que decimos es que en los textos que analizamos, de cada 100 letras 14 son e y en segundo lugar viene la letra a con 12,5 veces. Pero ¿cómo puede ser que una letra aparezca media vez? Bueno, acá lo expresamos como una proporción para que sea más simple de leer que el gigante número anterior. Es la misma idea que cuando calculamos el promedio de notas, si nos sacamos 8, 8, 8 y 9, nos dará que tenemos un promedio de 8,25, aunque nunca nos sacamos esa nota.
Volviendo a nuestro problema, en orden de aparición las letras que más aparecieron fueron e, a, o, s, r, n, i, d, l, c, t, u, m, p, b, g. Las que faltan ocurren menos de 1 vez cada 100 letras en promedio.
Con esta información y con el mensaje encriptado, les invitamos entonces a agarrar lápiz y papel y descubrir que es posible, sabiendo el idioma y su forma de uso, romper el código con el que se cifró el mensaje y leerlo.
Corolario
Cualquiera que conozca el idioma del mensaje enviado podrá desencriptarlo usando las tablas de frecuencia de aparición de las letras. Es por esto que los mecanismos de encriptación actuales no recurren a cambiar una letra por otra para ocultar un mensaje, sino que encriptan con algoritmos que miran los bytes detrás del mensaje entero, y los cambian utilizando una clave o contraseña, sin la cual es muy difícil desencriptarlos.
¿Cómo se reparten los primos?
En nuestra edición de #TeRegaloUnTeorema de hoy vimos que existen infinitos números primos.
Hagamos al 2 a un lado, ya que salvo él todos los primos son impares. (Hay un dicho popular en inglés sobre los primos, que juega con que odd significa a la vez impar y raro. Dice: Primes are odd, and two is the oddest prime of all).
Si tengo un primo (impar), lo puedo dividir entre 4 y fijarme cuánto da el resto. Por ejemplo:
17 = 4 * 4 + 1 -> resto 1
23 = 4 * 5 + 3 -> resto 3
Podemos así repartir a los primos impares en dos conjuntos:
U = primos que al dividirse por 4 dan resto 1
T = primos que al dividirse por 4 dan resto 3
Alguno de los dos tiene que ser infinito, porque en caso contrario el conjunto de los números primos sería finito. La pregunta natural que surge es la siguiente: ¿serán ambos infinitos? ¿O alguno de ellos será finito?
Experimentemos. Proponemos un ejercicio para el lector que sepa un mínimo de programación (o menos aún, que tenga ganas de aprender): definir dos funciones que, dado un número n, calculen los siguientes valores:
u (n) = # {primos menores que n, que pertenecen a U} / # {primos impares menores que n}
t (n) = # {primos menores que n, que pertenecen a T} / # {primos impares menores que n}
Por ejemplo:
u (30) = # {5, 13, 17, 29} / # {3, 5, 7, 11, 13, 17, 19, 23, 29} = 0,444…
Se puede implementar online, por ejemplo usando Python en:
www.pythonanywhere.com/try-ipython/
Calcular restos es así de sencillo:
In [1]: 23% 4
Out[1]: 3
Para trabajar con números primos, por ejemplo, la librería SymPy nos provee una función que nos devuelve el primo siguiente a un número dado:
In [2]: from sympy import nextprime
In [3]: nextprime(22)
Out[3]: 23
Volviendo a la teoría, estas funciones miden cómo se reparten, proporcionalmente, los primos en cada uno de los dos conjuntos.
Por ejemplo, si el conjunto U fuera finito entonces la función u va a dar cada vez más cercana a 0 cuando la evaluemos en números cada vez más grandes, pues su denominador va a crecer (ya que hay infinitos primos) pero su numerador quedará acotado. Podríamos decir en tal caso que 0% de los primos pertenecen a U (sin que esto signifique que U sea vacío: por ejemplo, 5, 13, 17, etc., pertenecen a U) mientras que 100% de los primos pertenecen a T.
Supongamos que por el contrario fueran ambos infinitos. Si sucediera, por ejemplo, que evaluando u en números cada vez más grandes obtuviéramos valores cada vez más próximos a 0,4 y evaluando t en números cada vez más grandes obtuviéramos valores cada vez más próximos a 0,6, podríamos decir que el 40% de los primos pertenecen a U mientras que el 60% de ellos pertenecen a T.
(Sin decir agua va, estamos hablando de porcentajes de un conjunto infinito. Este probablemente sea un concepto novedoso para el lector.)
A experimentar: proponemos al lector implementar ambas funciones y evaluarlas en números cada vez más grandes, para así conjeturar cuáles son estos porcentajes. Esperamos sus resultados en:
[email protected]
Cero en lógica
Hay un artículo antes que este que se llama ‘Cero lógica’. Me encantaría que la correctora de Ciencia Hoy analice el título y nos haga llegar un análisis detallado. No me extrañaría que –solo porque comienza hablando de la pandemia– el título corregido sea ‘Serológica’, lo cual estaría mal, pero no tan mal.
El punto interesante de la frase ‘cero lógica’ es todo lo que está implícito: lo entendemos como ‘no tiene lógica’, ‘no hay lógica’, ‘es ilógico’, y así está bien.
Pero si le preguntamos a un lógico cuántas lógicas conoce donde se acepte un axioma y su negación nos dirá que no hay ninguna: ‘cero lógicas’. Porque ¡dado que el cero es par, no le queda otra que ser plural! ‘Presentaron cero ideas’, ‘tenía cero conocimientos sobre el tema’, ‘sacó cero votos’, ‘hay cero grados de temperatura’ (centígrados, que si fueran Farenheit la radio no diría nada de nada de nada). Siga buscando ejemplos, coincidirá que es algo raro, pero así es la gramática del cero.
Y les dejo entonces otra duda gramatical: ¿qué hacemos con las fracciones? ¿Es igual en castellano o inglés? Otros idiomas se los debo, ¡si me envían ejemplos, se los voy a agradecer!
Soluciones
Cero lógica
No necesariamente, no dijo que es el único caso en que iría caminando.
No necesariamente, no dijo cómo iría si no comenzara por la tarde.
Verdadero, ya que si hubiera comenzado por la tarde, habría ido caminando.
La letra más usada
El mensaje desencriptado es:
15 de agosto de 2021
Querido nono Osvaldo, no olvides de mirar la Ciencia Hoy que hay que desencriptarla. Esta vez es más compleja que la anterior pero igual seguro sale. Nos vemos en casa. Un gran saludo, tu nieta Mercedes.
Cero en lógica
En castellano decimos las fracciones en singular: media porción, una empanada y media, hora y media, un cuarto de pizza, tres cuartos de la población… Pero en inglés, ‘one and a half men/hours’. Raro, más odd que el 2, ¿no?
Equipo de la sección ‘Ilusiones y juegos matemáticos’
Marilina Carena
Matemática, UNL-Conicet.
[email protected]
Nicolás Fernández Larrosa
Biólogo, IFIBYNE, UBA-Conicet.
[email protected]
Pablo Groisman
Matemático, UBA-Conicet.
[email protected]
Matías López-Rosenfeld
Computador, UBA-Conicet
[email protected]
Juan Pablo Pinasco
Matemático, UBA-Conicet.
[email protected]
Nicolás Pírez (coordinador)
Neurobiólogo, IFIBYNE, UBA-Conicet.
[email protected]
Alfredo Sanzo
Ingeniero, ICC, UBA-Conicet.
[email protected]
Nicolás Sirolli
Matemático, UBA-Conicet.
[email protected]
Preguntas, comentarios y sugerencias: [email protected]











