¿Puede un sistema regido por una ley exacta evolucionar con un arquetipo del azar, como el arrojar monedas a cara y seca ? Tal aparente paradoja se origina en la tensión entre dos idealizaciones: la de un punto en el espacio y la del tiempo infinito
Es sabido que parte de la correspondencia de Newton a Leibnitz consistió en un intercambio de anagramas (de anagrama, escrito hacia atrás, transposición de las letras de un texto para ocultar su mensaje). Se puede suponer que Newton eligió comunicar ciertos conocimientos de esa forma porque quiso tener cuidado y guardar la mayor reserva. Sin embargo, la historia no ha recogido cuál era el valioso conocimiento así transmitido por uno de los creadores del cálculo infinitesimal al otro, y – como consecuencia de ello o por otra causa – la física se ha empeñado durante años en desoír a Newton. Como preparación para revelar el significado de un anagrama de Newton que resulta particularmente adecuado para la física de hoy, permítasenos una breve digresión.
La ciencia construye su estructura sobre la creencia en la invariabilidad de las leyes naturales. Pero, como señaló Auguste Comte en 1844, en su Discurso sobre el método positivo, no existe razón alguna que fundamente esa invariabilidad; ni siquiera la hay para explicar la misma existencia de leyes naturales. Bien pudiera ser que la caída de una manzana arrojada desde la torre de Pisa se rigiera por la voluntad caprichosa y cambiante de un dios de las manzanas (o de uno de las torres), y que no estuviese sujeta a ley constante alguna. Sin embargo. la evidencia empírica no resulta demasiado inteligible a la luz del supuesto de las divinidades caprichosas, y se interpreta bastante bien con la hipótesis de las leyes naturales. De ahí resulta la capacidad fundamental de la ciencia, incluida la física, de predecir, una de cuyas más deslumbrantes manifestaciones se ejerció en el campo de la dinámica celeste, sustentada en las leyes de la mecánica clásica o newtoniana. En el siglo XIX, la capacidad de anticipar el movimiento de los astros y sus consecuencias visibles – eclipses y apariciones de cometas- influyeron fuertemente en las ideas, y en movimientos filosóficos como el positivismo.
Para poder realizar las predicciones a las que dan acceso las leyes físicas se requiere utilizar ciertos instrumentos de cálculo: en el caso de la mecánica clásica, para predecir el movimiento de los cuerpos celestes se necesita del cálculo infinitesimal de Leibnitz y Newton. Las leyes de la física y sus medios de cálculo forman un todo indisoluble, si bien su relaciones son de tipo dialéctico. El método de esta disciplina consiste, precisamente, en inducir ciertas leyes a partir de la observación del mundo y. para comprobar su validez, aplicarlas para predecir no sólo fenómenos como los que llevaron a formularlas sino, también, otros que les están relacionados. Una nueva ley o teoría se somete a infinidad de intentos de predicción de resultados, para lo cual se usan métodos de cálculo que toman forma en constante interacción con el proceso de inducir leyes. A lo largo de la historia de la ciencia, algunas parejas de leyes naturales con métodos de análisis se han vuelto paradigmáticas; además de la dupla mecánica clásica – cálculo infinitesimal, piénsese en las de mecánica cuántica – espacios de Hilbert y. como veremos, caostopología.
La posibilidad de tener un mundo absolutamente predecible está sujeta a algunas limitaciones. En el orden práctico, nuestra capacidad de predecir está limitada por la de observar: a una observación inexacta corresponde una predicción inexacta. Se trata de una limitación extrínseca, pues no resulta de la ley sino de nuestra capacidad de hacer uso de ella, la que puede aumentarse mediante otro recurso de cálculo: el proporcionado por la teoría de la probabilidad. Con el advenimiento de la mecánica cuántica y su interpretación en términos probabilísticos por la escuela de Copenhague, la imagen de un mundo físico completamente predecible sufrió una modificación substancial, pero en el mundo macroscópico, donde las correcciones cuánticas son despreciables, en general tal imagen conserva su validez.
La limitación de las predicciones debido al margen de error que, con mayor o menor probabilidad, caracteriza a toda observación física sólo parece constituir un problema práctico, sin consecuencias serias para la ciencia, aunque tal vez las tenga para sus aplicaciones. Pero el asunto no termina ahí. Consideremos la estabilidad del sistema planetario, el que se puede describir con muy buena aproximación mediante las leyes de la mecánica newtoniana. Podemos preguntarnos si los planetas seguirán girando en sus órbitas alrededor del Sol como lo hacen ahora o sí, con el tiempo, el sistema se desintegrará y se dispersarán las masas que hoy lo componen. Dado que sólo tenemos un conocimiento aproximado de la distribución y velocidades de esas masas – y no es esperable que alguna vez alcancemos uno exacto – , debemos conformarnos con una respuesta a menos de nuestro desconocimiento, es decir, que no dependa de la parte del problema que desconocemos.
La mayor influencia sobre el sistema Tierra – Luna es ejercida por el Sol. Tomando únicamente esa influencia, nos podríamos preguntar sí la órbita real de aquel sistema se ajustará por siempre a lo calculado mediante los datos que hayamos podido obtener, tan precisos como sea posible pero nunca exactos. La respuesta estará afectada por dos incertidumbres: la que ocasione el tener un conocimiento sólo aproximado de las posiciones y velocidades de la Tierra, el Sol y la Luna, y la debida a no tomar en cuenta las influencias de otros astros (u otras masas) del universo. La primera se conoce como inestabilidad de las trayectorias; la segunda se refiere a objetos ajenos al modelo teórico y de cálculo, ya que decidimos no considerar más que la influencia del Sol, por lo que se relaciona con la estabilidad estructural del modelo predictivo.
A partir de Newton, el estudio de la dinámica celeste y. en especial, la predicción de los movimientos del sistema solar, constituyeron la ocupación central de físicos y matemáticos. Una serie impresionante de éxitos confirmó la potencia del método y contribuyó a crear una elegante y sólida estructura matemática, basada en el cálculo infinitesimal y en sistemas de ecuaciones diferenciales, cuyo rango de aplicaciones parecía inacabable. Se predijo la reaparición de cometas, se calculó con precisión órbitas de planetas y se llegó a deducir la existencia de un planeta desconocido – que se llamó Neptuno – a partir de perturbaciones de otro modo inexplicables observadas en la órbita de Urano. La imagen del científico que, literalmente con lápiz y papel, efectúa algunos cálculos e indica el lugar preciso del cielo adonde apuntar el telescopio para ver aparecer un nuevo planeta. otorgó un aura de infalibilidad, que aún perdura, a las predicciones de la física.
Sin embargo, había un problema que no parecía solucionable por ningún método y que desafiaba a las más lúcidas mentes del siglo pasado: el de determinar las posiciones y velocidades de tres cuerpos que se mueven bajo la mutua atracción gravitatoria. Tiene cercana relación con la mencionada estabilidad del sistema planetario: a pesar de todo el instrumental matemático, no era posible predecir si, eventualmente, alguna conjunción de planetas podía resultar en la expulsión de uno de ellos o – aun más grave – en una colisión. El asunto llegó a preocupar tanto que el rey de Suecia instituyó un premio para el que lo resolviera y, aunque en realidad todavía no se ha logrado hacerlo, quien estuvo más cerca – y se llevó el premio fue Henri Poincaré.
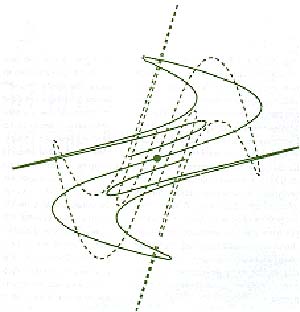
Poincaré buscó la solución con empecinamiento y, haciéndolo, encontró caminos que dieron lugar a nuevas ramas de las matemáticas. Así, el estudio cualitativo de las ecuaciones diferenciales, al cual recurrió para compensar los márgenes de incertidumbre contenidos en los modelos y en las condiciones iniciales, dio origen a la topología, que luego tomaría rumbos propios. Uno de sus resultados más intrigantes, precursor de los modernos estudios del caos, es la madeja homoclínica, una complicada figura que representa soluciones relacionadas con órbitas periódicas. Su descripción de este objeto ilustra las dificultades del problema: …uno queda impresionado por la complejidad de esta figura, que ni siquiera intentaré dibujar. Nada es más adecuado para ilustrar la naturaleza múltiple del problema de tres cuerpos y de todos los problemas generales de la dinámica… En la actualidad, con las computadoras, es relativamente sencillo trazar la figura 1, pero no se puede dejar de reconocer el genio de Poincaré, que logró imaginársela sin dibujarla y consiguió demostrar que en los intersticios de sus innumerables intersecciones hay infinitas nuevas órbitas periódicas inestables, que a su vez crean nuevas intersecciones, y así sucesivamente sin limite. Sobre la observación de Poincaré trabajaron Birkoff y j. von Neumann; este y B. O. Koopman, cuando desarrollaron la teoría ergódica, utilizaron por primera vez el término caos.
Para los físicos y matemáticos de fines del siglo pasado estaba claro que había muchos problemas sin solucionar en la dinámica newtoniana. Sin embargo, la física estaba a punto de dar un vuelco fundamental que los hizo caer en el olvido, pues a principios del siglo XX la atención se centró en lo inmensamente pequeño y lo inmensamente grande, es decir, en la física atómica (luego nuclear, luego subnuclear, luego…) y en la relatividad general, que desplazaron del centro de la escena de la física a los problemas de la dinámica y la mecánica clásicas. Estas pasaron a ser un capitulo en apariencia completo, conservado sobre todo por su valor formativo para la nueva física, pero desprovisto de interés como tema de investigación. Aquellas preguntas sin respuesta quedaron, simplemente, olvidadas, pues nadie parecía interesarse por ellas y, además, eran irrelevantes para el entrenamiento que debía proporcionar la dinámica.
Los éxitos predictivos de la mecánica cuántica y de la relatividad tuvieron el mismo efecto que, en el siglo anterior, habían tenido los de la mecánica celeste. La mayoría de los físicos adoptó los nuevos enfoques y sus instrumentos matemáticos. El espacio de Hilbert reemplazó al de fases como arena de la dinámica, y su estructura, eminentemente lineal, excluyó a los fenómenos no lineales que Poincaré había comenzado a vislumbrar. El punto de vista y los objetos de estudio cambiaron radicalmente: el cálculo de las trayectorias de los planetas fue desplazado por las funciones de onda y los niveles de energía de átomos y núcleos. El problema de los tres cuerpos y las complicaciones de la madeja homoclínica no estaban, ciertamente, entre los temas de avanzada.
Durante la década de los sesenta se produjo un retorno a la dinámica no lineal. En 1963, E. N. Lorenz estudiaba un modelo esquemático de convección atmosférica y resolvía sus ecuaciones mediante técnicas numéricas, con la ayuda de una computadora. En algún momento debió interrumpir su cálculo; con el propósito de recomenzarlo, tomó la solución numérica a la que había llegado antes de detenerse y la consideró definitoria de nuevas condiciones iniciales, para así empalmar el nuevo cálculo de manera suave con el precedente. Echó a andar otra vez el procedimiento numérico y descubrió que, en la parte en que ambos cálculos se superponían, en lugar de dar los mismos resultados, arrojaban soluciones que divergían fuertemente a medida que avanzaba el proceso. Había caído, sin saberlo, en un régimen inestable debido a una situación de sensibilidad a las condiciones iniciales. En realidad, las nuevas condiciones iniciales diferían de los datos que venía utilizando la computadora antes de la interrupción, por el redondeo que resultaba en el momento de imprimirlos. Las trayectorias ulteriores de los valores exactos conservados en la memoria de la máquina y los inexactos que habían sido impresos magnificaban sus pequeñas diferencias iniciales y, con el tiempo, alejaban los resultados entre sí poco menos que sin limite.
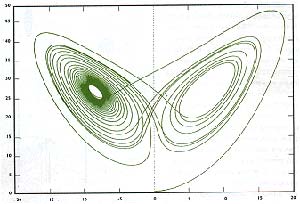
La dinámica encontrada por Lorenz no correspondía a una situación de punto fijo, en la que las variables toman valores constantes, ni a una de órbita periódica, en la que retoman los mismos valores en intervalos temporales regulares. No correspondía, en realidad, a nada que los físicos reconocieran y resultaba por demás extraña, nombre con el que empezó a ser conocida. Una vez identificado el nuevo fenómeno, los matemáticos lo formalizaron y ahora se lo conoce, precisamente, como atractor extraño. Tal tipo de comportamiento ha sido encontrado en otros procesos dinámicos del más variado tipo: en ciclos económicos, en reacciones químicas, en la evolución de poblaciones y en la epidemiología de enfermedades infecciosas. En la figura 2 se puede ver una imagen del atractor de Lorenz.
La magnitud de la sorpresa de Lorenz y del resto de la comunidad científica estaba en proporción con el olvido en que se encontraban los trabajos de Poincaré. La imagen que inmortalizó el descubrimiento de Lorenz es el llamado efecto mariposa (butterfly effect), que puede describirse diciendo que sí uno de esos insectos agita suavemente sus alas en China, se puede llegar a producir un ciclón en San Francisco.
Otro descubrimiento de la década de los sesenta que dio lugar al renacer de la dinámica no lineal es atribuible a S. Smale, quien, en un estudio cualitativo, propuso un modelo que rescataba la esencia geométrica y topológíca de la trayectoria homoclínica de Poincaré. Dicho modelo, llamado herradura de Smale e ilustrado en la figura 3, consiste en representar los estados posibles de un problema por puntos encerrados en un cuadrado, que es luego comprimido horizontalmente a la mitad, estirado verticalmente al doble y, finalmente, cortado en dos para reordenar las partes de forma que se reconstruya el cuadrado, de manera parecida a lo que hace un panadero cuando estira la masa, la dobla, la vuelve a estirar… Cada vez que tiene lugar un ciclo de operaciones se dice que se ha avanzado una unidad de tiempo.
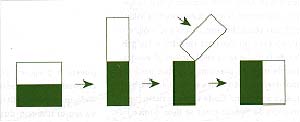
El modelo de Smale tiene la virtud de hacer manifiesta la rápida pérdida de nuestra habilidad predictiva con el paso del tiempo. Supongamos, por ejemplo, que las condiciones iniciales de nuestro sistema o problema se encuentran representadas por el circulo negro de la figura 4. Transcurrida una unidad de tiempo (n=.l), el circulo se deforma pero se mantiene cerca de donde estaba; con las sucesivas unidades, se fragmenta en muchas franjas verticales, de suerte que puntos inicialmente vecinos se apartan y, eventualmente, se dispersan uniformemente por todo el cuadrado. Visualmente, después de transcurridas muchas unidades de tiempo (n muy grande), el circulo negro en el cuadrado blanco se habrá transformado en un cuadrado uniformemente gris.
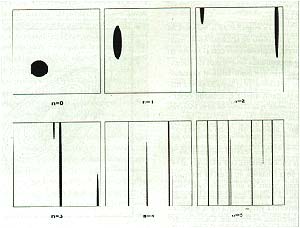
Partiendo de determinada información inicial sobre la localización del sistema, luego de transcurridas algunas unidades de tiempo (n>2) deja de tener respuesta la pregunta acerca del cuarto del cuadrado en que podría encontrarse aquel, dado que podría hallarse en cualquiera. Nada mejoraría con determinar con mayor precisión la ubicación inicial, pues siempre se llegaría al momento en el que no seria posible determinar el cuadrante de ubicación del sistema. Smale demostró que la dinámica de su sistema es indistinguible de la secuencia de caras y cecas que se obtiene arrojando monedas: para cada secuencia de caras y cecas existe una trayectoria posible del sistema.
Sí el sistema, y por ende su evolución, está regido por una ley exacta y determinada, ¿por qué está relacionado con un arquetipo del azar, como el arrojar monedas a cara y ceca? Tal aparente paradoja se origina en la tensión entre dos idealizaciones: la de un punto en el espacio y la del tiempo infinito. Ambas representan los límites ideales de situaciones físicamente realizables, pero el orden de estas idealizaciones determina que el resultado se rija por el azar o el determinismo.
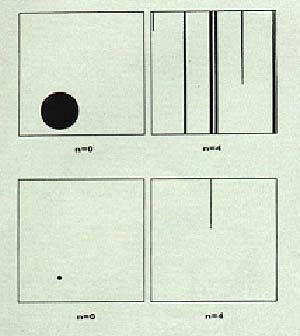
No puede continuarse con la ilusión clásica de una trayectoria representativa de todas las cercanas a ella, en todos los tiempos. Dado un tiempo suficientemente largo, en una dinámica caótica las trayectorias de puntos que comenzaron formando parte de una pequeña mancha se apartarán de la de cualquier otro punto que se haya adoptado como testigo (digamos, uno ubicado inicialmente en el centro de la mancha). En la figura 5 se compara la evolución de una mancha grande con una pequeña: en un tiempo fijo (n=4), la pequeña mantiene su localización, cosa que no le sucede a la grande. Extrapolando esta situación, puede advertirse que, para cualquier tamaño inicial, siempre habrá un tiempo al cabo del cual se desconocerá el estado del sistema; e, inversamente, para un tiempo fijo de evolución, siempre se podrá reducir el tamaño de la mancha de manera de no perder el poder predictivo. En el lenguaje de las matemáticas, el limite de tiempo infinito y el de infinita precisión no son conmutables. El orden de las idealizaciones es, en este caso, relevante.
En una situación real caracterizada por precisión finita y tiempo finito podemos estar cerca de uno de los casos limite. Importa saber el costo de predecir, porque el caos, en esencia, cambia ese costo. Sí en los casos no caóticos, para extender una predicción (con igual precisión) de un tiempo T a otro n veces más largo, nT, se requiere mejorar la determinación inicial por un factor proporcional a n, en el caso caótico debemos mejorarla por un factor que crece exponencialmente con n, o ln. Para tiempos largos, el costo de la predicción puede llegar a ser prohibitivo, más allá de que nuestros aparatos puedan lograrla.
¿En qué medida persistirá el caos ante pequeños cambios del modelo? Sí, acaso, la existencia del caos dependiera de las características particulares de los modelos, y pudiera desaparecer ante una pequeña corrección de estos, la relevancia de esa dinámica no lineal seria cuestionable, dado que todo modelo físico está diseñado para que sus resultados no dependan de la necesidad de realizar esas correcciones (dícese que está determinado a menos de correcciones menores – y a veces no tan menores-). Pero las estructuras de órbitas homoclínicas que dan lugar a dinámicas como la de la herradura de Smale persisten ante correcciones o perturbaciones del sistema. Por lo tanto, sí se encuentra uno en el que se advierten fenómenos caóticos, se los advertirá también en otros cercanos a él. Sí aplicáramos este resultado al sistema de Lorenz, encontraríamos que una pequeña variación en la temperatura de la atmósfera o la consideración de algún efecto menor en las ecuaciones no harían desaparecer el comportamiento caótico: el aletear de la mariposa seguirá produciendo el ciclón, pero este podría ocurrir en Chile en vez de en California.

¿Cuán frecuente es el caos en la naturaleza? La respuesta es terminante: si se elige al azar un sistema dinámico, es prácticamente seguro que tendrá algún tipo de comportamiento caótico; este, pues, constituye la regla y no la excepción. Los sistemas caracterizados por un comportamiento regular – como un planeta que gira alrededor del sol – y, por lo tanto, predecible, forman un minúsculo conjunto. El pequeño escollo encontrado por Poincarè y olvidado durante medio siglo resultó la punta de un iceberg.
El final del siglo XX está dominado por la matemática de Poincaré y la dinámica no lineal, cuya importancia y ubicuidad resultan innegables. La existencia de comportamientos caóticos se ha comprobado en láseres, fluidos, reacciones químicas y procesos biológicos, y se busca confirmar su presencia en sistemas ecológicos, económicos, sociales y artísticos. En la física, la dinámica clásica se ha tomado una suerte de revancha de la cuántica: los proyectiles con que se explora el mundo subatómico en los grandes aceleradores se comportan caóticamente. Así, el conocimiento del caos condiciona el entendimiento del mundo microscópico.
Por ello viene al caso uno de los anagramas de Newton:
Data aequatione quotcunque fluentes quantitae involvente fluxiones invenire et vice versa
De acuerdo con la traducción al lenguaje científico moderno, realizada por V. I. Arnold, uno de los más grandes conocedores de la obra de Newton, significa:
It is useful to salve differential equations.











