Tres problemas matemáticos, muy sencillos de plantear, pero para los que todavía no hay solución.
Una esfera, un velador y un sofá pueden
generar situaciones a las que no resulte
sencillo encontrarles una respuesta
El conjunto integrado por los redactores y colaboradores de CIENCIA HOY, constituye una comunidad heterogénea donde, sin embargo, se observa que los matemáticos parecen estar en franca minoría. Esto se debe quizás a un cierto tipo de postura, que frecuentemente es adoptada a priori por muchos de los pocos matemáticos argentinos. Ella supone -a mi juicio, sin mayor fundamento – que es muy difícil exhibir, divulgar o discutir problemas matemáticos contemporáneos con especialistas de otras disciplinas. ¿Será tal vez que estas, por su propia naturaleza, están algo alejadas del álgebra o del análisis usualmente requeridos para la consideración provechosa de los problemas citados? En principio, esta circunstancia en si no es sorprendente, y sugiere realizar consideraciones que no son triviales en absoluto.
De hecho, el nivel de especialización que hoy día tienen las Ciencias Matemáticas hace bastante difícil el intercambio de información inteligible entre los mismos matemáticos activos en sus diferentes áreas de trabajo. Por ejemplo, entre topólogos y geómetras algebraicos, o entre matemáticos aplicados y algebristas.
¿Tendrá sentido entonces hablarles de Matemáticas actuales a un geólogo, a una bióloga o a un grupo de paleontólogos inquietos? Más aún: ¿quedará espacio en esta hipotética convocatoria para los sociólogos, médicos, psicólogos o abogados?
En este artículo, intentaré alcanzar el objetivo que plantea la posibilidad del intercambio de información matemática, no solamente entre matemáticos activos, sino entre científicos o profesionales que no lo son. Que el objetivo enunciado parezca difícil de ninguna manera implica que lo sea.
En efecto, la búsqueda entusiasta e intensa de bibliografía adecuada revela la existencia de una multitud de problemas matemáticos que son a la vez fáciles de formular, de interés actual y, en la mayoría de los casos, muy difíciles de resolver. Por estas razones resultan un desafio interesante para cualquier persona con perspicacia e inquietudes matemáticas. Aunque fuese como motivo de reflexión o recreación momentánea. Aunque el lector no sea matemático.
Describiré entonces, a continuación, tres ejemplos cuidadosamente elegidos y presentados: casi sin cálculos y sin fórmulas. Pero tratando de insinuar las matemáticas (muy complejas) que subyacen tras el análisis efectuado sobre objetos comunes: una esfera, un velador intermitente y un sofá que necesita cambiarse de lugar.
Apenas quizás pueda considerarse provechosa la realización de unos pocos dibujos que el lector juzgue conveniente realizar a mano alzada, tal como posiblemente lo exija el problema del mencionado sofá.
La esfera de Ulam
Stanislaw Ulam, otro investigador en la Universidad de Colorado, fue uno de los matemáticos norteamericanos más brillantes de los que actuaran hacia la mitad del siglo XX (Bali, edición de 1995). Colaboró con John von Neumann – uno de los padres de la computadora digital-, en el desarrollo del llamado “Método de Monte Carlo”, que incorpora técnicas aleatorias en el tratamiento de problemas numéricos, clásicamente encarados mediante el auxilio de ecuaciones diferenciales.
El siguiente ejemplo muestra la personalidad y jerarquía de Ulam, quien jamás rechazó el desafio que plantean algunos temas considerados elementales (existe consenso generalizado entre los especialistas en el sentido de que “elemental” no es sinónimo de “fácil”).
A los matemáticos les gusta decir que la circunferencia y la esfera son la misma entidad, pero condenadas por la cruda naturaleza de los hechos a vivir en universos diferentes: uno plano y otro no tanto. Los investigadores que cultivan el análisis funcional y algunas otras especialidades afines, llaman a la esfera de muchas maneras graciosas, que se toleran estrictamente en un contexto técnico, pero nada más que allí. Es posible referirse a esa entidad como “la frontera del rentorno dada por la imagen difeomórfica de una afinidad ortogonal aplicada sobre la frontera de la bola unitaria euclídea”. Si el lector no matemático piensa que esto es una tontería, es probable que tenga razón.
Ruego ahora pasar urgentemente al estado de alerta roja para lo que sigue. Resultará familiar para todos la experiencia infantil de haber jugado, por lo menos una vez, con una pelota de goma en la bañadera. Cito las bañaderas y no las piletas de natación, porque las primeras tienen un bien ganado y conocido prestigio en la Historia de la Ciencia. Se recordará que, en Siracusa, el genio de Arquímedes las hizo famosas luego de una reflexión sutil y acertada que surgió precisamente durante el baño en su bañadera. Descubrió allí su clásico principio hidrostático anunciándolo al mundo a través de sus alaridos.
El hecho es que una esfera homogénea cuyo peso especifico sea r, con r < 1 (le asignamos al agua peso específico r=1 en algún sistema de unidades, por ejemplo g/cm3 o kg/dm3) estará obligada a flotar cómodamente en toda bañadera llena de agua. Y además, flotará en equilibrio indiferente no importa la posición en que se la coloque. De manera provisoria, llamemos a esta propiedad PEI ("propiedad de equiflotabilidad isotrópica").
A mediados de 1960, Ulam puso en aprietos a la comunidad internacional de sus colegas cuando preguntó abiertamente si existirán otros cuerpos, además de la esfera, con la propiedad PEL Luego de un intrigante periodo de silencio, los matemáticos que recogieron el guante arrojado por Ulam, vieron con claridad que si la respuesta fuese negativa, entonces la propiedad PEI habría de caracterizar a las esferas flotantes de una manera inequívoca hasta entonces desconocida. Si por el contrario, la respuesta fuese positiva, debería en este caso exhibirse de manera imperativa un cuerpo no esférico -y no vislumbrado para nada-, con la ya mencionada propiedad PEI.
Hasta la fecha (1998), nadie ha dado una respuesta completa al desafio, aunque debe decirse que se obtuvieron algunas aproximaciones muy laboriosas. Por citar un ejemplo, en 1983 Falconer demostró que un cuerpo con simetría central fabricado con un material cuyo r sea 0,5 y que goce de la propiedad PEI, es efectivamente una esfera. Las consideraciones de este trabajo son extensas pero legibles.
El interrogante planteado por Ulam está netamente abierto, ya que existen todavía infinitos valores del peso especifico r en el intervalo abierto (0,1) distintos de 0,5. Con el correr de los años, algunos autores, Montejano por ejemplo, han sospechado que la propiedad PEI es exclusiva de la esfera y de ningún otro cuerpo más. Pero como se comprenderá, las sospechas o creencias personales de las autoridades en Ciencias Matemáticas, por más grandes que éstas sean -y a las que se asigna “criterio de autoridad”-, no interesa a los matemáticos más que como meros detalles de carácter anecdótico.
El velador de Thompson
Los filósofos de la ciencia como Gale en 1978, y algunos físico-matemáticos destacados como De Witt-Graham en 1973, discutieron la cuestión planteada hacia mediados de 1950 por el naturalista norteamericano J. Thompson (1905-1973). El asunto – no resuelto hasta la fecha – puede describirse básicamente como sigue.
Sea un velador con un interruptor común y corriente, que permita apagarlo y encenderlo a voluntad. El artefacto se enciende durante un minuto, se apaga luego durante medio minuto, se vuelve a encender durante el cuarto de minuto que sigue, a continuación se apaga durante el octavo de minuto contiguo y así sucesivamente de manera alternada. Si esta serie de prendidos y apagados fuera realizable, se puede demostrar con rigor que duraría un total de dos minutos. En esta última hipótesis, se pregunta entonces cuál será al cabo de ese intervalo el estado del velador. ¿Estará prendido o apagado?
Este extraño problema parece seguir la línea trazada por aquel clásico sofisma griego, de los que planteaba Zenón hacia el siglo V a.C., conocido como la “paradoja del arquero”. En esta cuestión, un soldado de infantería tensa al máximo su arco apuntando sobre un blanco ubicado a dos pasos de distancia, y lanza luego hacia allí una flecha perfectamente dirigida que, según el sofista, nunca llegará a su destino. El argumento empleado es conocido y puede exponerse como sigue. El proyectil no tocará el blanco porque, antes de alcanzarlo, deberá recorrer una cantidad infinita de segmentos, siendo la longitud de cada uno la mitad de la longitud que queda por recorrer. La paradoja se resuelve en la actualidad, mostrando que el intervalo de longitud “2 pasos” puede presentarse realizado como una serie geométrica de razón – (igual a “medio paso”), es decir como una suma infinita de segmentos de longitud (_)n de paso, con n>=0, cuya suma es precisamente 2 pasos. La sucesión de intervalos tendría longitudes “1 paso” (n=0, “medio paso” (n-1), “un cuarto de paso” (n-2), etc. El mismo argumento se aplica al intervalo de tiempo que le lleva a la flecha recorrer cada intervalo; la suma infinita de estos tiempos no será un tiempo infinito sino un intervalo finito al cabo del cual la flecha hará blanco. Cabe consignar aquí que los elementos implícitos en la respuesta dada no estaban disponibles en la época de Zenón. Como se sabe, esos elementos comenzaron a sistematizarse de manera simultánea a partir del siglo XVII, mediante la obra de Newton y Leibniz, quienes entre otros aportes fundamentales, desarrollaron el algoritmo conocido como “paso al límite”. Tal concepto constituye el punto de partida para la enorme construcción posterior que hoy se designa como Análisis Matemático.
Volviendo al velador de Thompson, la lógica del problema se hace más evidente al notar lo siguiente. Durante cada pulsación de turno impar, el velador estará encendido y durante los turnos pares estará apagado. Parece indudable que al cabo de dos minutos deberá estar, o bien encendido o, de lo contrario. Sí sucede lo primero, entonces el último número natural seria par. Si el resultado fuese el segundo, el último natural seria impar. Pero, como se sabe, no hay un último número natural.
El planteo nos lleva a preguntarnos si será correcto utilizar una lógica bivalente. Es decir, ¿será verdad que al cabo de dos minutos el velador estará prendido o apagado? En su libro Paradojas que Hacen Pensar (Barcelona, Labor, 1984) Martin Gardner comente otras perturbadoras variantes del tema, y sugiere la plausibilidad de estudiarlo en un contexto lógico polivalente, es decir con más posibilidades que las dos enunciadas más arriba. Así y todo nunca llega a dar una respuesta definitiva al interrogante. El problema de Thompson permanece abierto.
El problema del sofá
Al insistir con las experiencias propias de le vida diaria, muchos lectores habrán tenido serios contratiempos cuando en una mudanza ellos o sus familiares, sintieron la necesidad de trasladar un sofá a otra parte de la cesa. Al intentar tan incómoda operación es común toperse de golpe con el sorpresivo calvario de tener que hacerlo pasar por un incomodisimo pasillo en ángulo recto, interpuesto de modo muy desagradable en le trayectoria por supererse.
Esta cuestión, aparentemente inofensiva a pesar de su molesta incidencia, es muy complicada desde el punto de viste matemático. Se treta de otro problema abierto en el sentido siguiente: no se sabe a ciencia cierta cuál es el sofá de mayor planta, o área, que puede hacerse pasar a través de un pasillo en ángulo recto con ancho unitario en sus dos brazos, sin dañar el mueble y sin rayar las paredes del pasillo, ¡supuestemente recién pintado!
Estimo necesario señalar que las vicisitudes inherentes a este problema no constituyen un pasatiempo trivial o un mero acertijo de ingenio.
El tema debería interesar bastante a los administradores gubernamentales de Salud Pública, como así también a los arquitectos e ingenieros que actúan en ese ámbito tan críticamente útil. Vale la pena recordar aquí, específicamente, una penosa realidad de dominio público. En efecto, existe un inmenso edificio color crema construido para albergar las instalaciones del nuevo Hospital Municipal de San Isidro -ubicado sobre la avenida Centenario en el tradicional partido homónimo al norte de la ciudad de Buenos Aires-, nunca pudo llegar a inaugurarse. Entre otras dificultades técnicas padecidas por esa construcción, se destacan los pasillos en ángulo recto que unen sectores afectados al tratamiento de pacientes en internación. Fueron construidos de manera tal que no admiten el tránsito de las camillas de dimensiones normalizadas ofrecidas por el mercado local del ramo.
Con el objeto de revelar lo que los autores hispanohablantes denominan el estado del arte vinculado al tema, incluyo dos variantes con propuestas aproximadas a la solución óptima del problema: un sofá en un trance como el comentado inicialmente (fig.1a), y otro frente a la disyuntiva planteada por un pasillo que se bifurca transversalmente en forma de T (fig.1b).
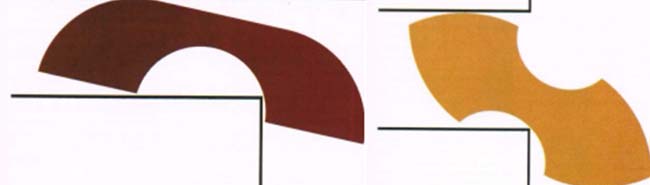Izq: Fig.1a. Aproximación al problema del sófa dado por los matemáticos Francis y Guy. Der: Fig.1b. Aproximación al problema del sófapara un pasillo en forma de T dada por Conway
Hay una versión unidimensional de la cuestión inicialmente planteada. Es mucho más simple, aunque tampoco inmediata, expresándonos en términos analíticos.
Interesa determinar el largo máximo de una varilla rígida (no flexible e indeformable) que también necesita hacerse pesar por el mismo tipo de pasillo exigido para el sofá. Piénsese por ejemplo en un caño de desagu’e, en una escalera de pintor inderformable, o tal vez en un largo rectángulo de vidrio pensado pare cubrir un ventiluz.
¿Cuál será el valor máximo de esta longitud?
Conclusión
Las Matemáticas están en realidad muy impregnadas de cuestiones como las presentadas brevemente en este trabejo. De acuerdo con lo señalado por el Dr. Luis Santeló, en sus inolvidables clases de Complementos de Álgebra y Topología desarrolladas hacia 1976 en la Facultad de Ciencias Exactas de la UNBA, hay dos categorías de problemas matemáticos:
a) Los que requieren mucha información previa, tanto pare captar su esencia como para luego intentar resolverlos.
b) Los que requieren poca información para lo mismo.
Ahora bien, siempre según el mismo autor, que además de sus conocidas inquietudes pedagógicas y didácticas es considerado uno de los matemáticos que más ha contribuido al desarrollo de la extensa y compleja teoría conocida como Geometría Integral, cada una de las categorías citadas tiene a su vez dos subclases: la de los problemas fáciles y la de los problemas difíciles. Los primeros requieren poco tiempo para su resolución, y los segundos pueden requerir muchísimo.
Los problemas aquí expuestos, requieren ciertamente poca información para entender su esencia y a la vez, son también muy difíciles. De hecho, los tres permanecen aún abiertos. La búsqueda bibliográfica a la que aludí en la introducción del presente artículo estuvo orientada por una muy acertada clasificación formulada por el distinguido maestro catalán. Más aún: en el mismo estilo de los tres ejemplos enunciados, existe toda una literatura extensa y creciente de problemas fáciles de entender y formular, asimismo muy difíciles de resolver, y en muchos casos también sin solución a la vista.
Quizás, los ejemplos expuestos puedan capturar -aunque sea de manera mínima- el interés de los lectores no matemáticos. Y debo afirmar también: tal vez atraigan la atención de los lectores que silo son, aunque insistan en esconderse cotidianamente en los ininteligibles laberintos de su actividad específica.
