El cielo del Hemisferio Sur, cómo se lo espera durante los próximos siete meses (hasta mayo de 1998).
El capítulo de la física que conocemos con el nombre de Teoría de la Relatividad se divide en dos grandes secciones: la relatividad especial (o restringida), que ha alcanzado amplia divulgación; y la relatividad general. En la relatividad especial (1905), Einstein necesitó modificar nuestra creencia en la independencia del observador en la medida de tiempos, con el ánimo de otorgar a las leyes del electromagnetismo la categoría de leyes fundamen tales -válidas en cualquier sistema de referencia (o laboratorio) inercial-. Nuestras nociones intuitivas de espacio y de tiempo se modificaron de forma tal que resultaron ser válidas sólo en el rango de velocidades pequeñas comparadas con la de la luz; una situación típica de nuestra experiencia cotidiana. El espacio y el tiempo absolutos de Newton fueron reemplazados por un nuevo absoluto: el espacio-tiempo relativista. Sin embargo, el nuevo espacio-tiempo no perdió su carácter de escenario inmutable en donde suceden los fenómenos físicos: el espacio-tiempo era sede de los fenómenos pero no era modificado por ellos; era escenario pero no actor. En 1916, con la relatividad general, Einstein promovió el espacio-tiempo a la categoría de “actor”.
La relatividad general es a la vez la teoría relativista del campo gravítatorio, y también la teoría en la cual desaparece el privilegio, sin origen aparente, de los laboratorios inerciales (según Newton, aquellos que se trasladan con movimiento rectilíneo y uniforme respecto del espacio absoluto). En la física newtoniana, la descripción de los fenómenos desde un sistema no inercial (por ejemplo, un laboratorio que rota respecto del espacio absoluto) requiere la inclusión de fuerzas ficticias, en el sentido de que no son debidas a una interacción; un ejemplo de ellas es la fuerza centrífuga. Estas fuerzas son proporcionales a la masa, como lo es la fuerza gravitatoria. Este hecho bien conocido le sugirió a Einstein que ambos tipos de fuerzas -las ficticias de los sistemas no inerciales y las gravitatorias-podrían tratarse como un único campo gravitatorio -inercial. Además, la formulación relativista de la gravedad también respondería al problema del privilegio de los sistemas inerciales, en el sentido de que se podrían formular las leyes de la física de manera que fuesen válidas en cualquier laboratorio (Principio de relatividad general).
Para formular su teoría del campo gravitatorio-inercial, Einstein produjo una nueva revolución en nuestra forma de ver el espacio-tiempo. En efecto, los fenómenos gravitatorios dejaron de modelarse mediante la acción de fuerzas provenientes de cuerpos masivos, para ser vistos como la consecuencia de cambios en la geometría del espacio-tiempo que no estaría más predeterminada, sino que se modificaría por la presencia de esos mismos cuerpos. El científico se dio cuenta, además, de que las propiedades euclidianas atribuidas a la geometría del espacio (o sea, un espacio chato donde dos rectas paralelas nunca se corten) eran tan sólo el reflejo de nuestra experiencia limitada a regiones pequeñas comparadas con escalas cosmológicas y alejadas de altas concentraciones de materia. No sólo las propiedades métricas del espacio, sino también la relación entre la marcha de un reloj y el decurso de la coordenada temporal resultan modificadas por la distribución de materia y energía, lo que también puede verse como un efecto geométrico sobre la coordenada temporal. En ausencia de fuerzas, los cuerpos siguen las trayectorias inerciales (las geodésicas) del espacio-tiempo curvado. Así, por ejemplo, el Sol curva el espacio-tiempo, y las órbitas de los planetas son las trayectorias naturales en esa geometría espacio-temporal curvada. A partir de Einstein sabemos que no sólo las distancias y los intervalos de tiempo no son absolutos sino que, el espacio-tiempo no es un escenario inmutable donde ocurren los fenómenos: el espacio-tiempo participa en los fenómenos. La geometría del espacio-tiempo es un actor más de la dinámica: es modificada por y modifica la distribución de materia y energía.
Hoy en día contamos con una fenomenología cada vez más rica asociada con las predicciones de la relatividad general. Las órbitas de los planetas, por ejemplo, no resultan ser perfectamente elípticas, como predice la teoría newtoniana. Este apartamiento es tanto más notorio cuanto más cercana sea la órbita a la fuente del campo (el Sol, en el caso de nuestro sistema planetario). Al poco tiempo de nacida la relatividad general se pudo demostrar que el movimiento de Mercurio estaba de acuerdo con la predicción relativista. Cabe destacar que la curvatura del espacio-tiempo afecta no sólo las trayectorias de los planetas, sino también las de los rayos de luz, un efecto que también fue verificado tempranamente (ver “La demostración sudamericana de las teorías de Einstein”, CIENCIA HOY 44, 50:59). En el orden cosmológico, los modelos de universo en expansión resultan de resolver las ecuaciones de Einstein. Una consecuencia de ellos es la existencia de una radiación cósmica de fondo -reliquia de la “sopa” de materia y energía a muy alta temperatura presente en los primeros instantes de la evolución- que ha sido detectada. En la actualidad, esta radiación se analiza con precisión creciente para extraer de ella información acerca de las inhomogeneidades que actuaron como semillas para la formación de estructuras en el universo. Se observaron también, imágenes múltiples de un mismo objeto celeste (mayormente cuásares) producidas por el efecto de “lente gravitatoria”. Se midió el retardo de señales de radio que pasan por la vecindad al Sol. Hay fuertes indicios sobre la existencia de agujeros negros.
En 1993 el Premio Nobel de Física fue concedido a Russel A. Hulse y Joseph H. Taylor Jr., por el estudio de la dinámica de un púlsar binario -descubierto por ellos mismos en 1974 que se convirtió en el test más preciso de la gravitación relativista. De acuerdo con la relatividad general, un sistema físico como el estudiado debe perder energía por emisión de ondas gravitatorias. Después de más de una década de trabajo, Hulse y Taylor verificaron que el comportamiento del púlsar binario se ajustaba perfectamente a las predicciones relativistas.
El efecto Lense-Thirring
En octubre de 1997, se anunció la medición del efecto Lense-Thirring producido por el movimiento rotatorio de la Tierra. Este efecto consiste en el “arrastre” de la estructura geométrica del espacio-tiempo debido al movimiento del cuerpo que origina al campo gravitatorio-inercial. Es como si hiciéramos girar una esfera dentro de un frasco con miel: la miel se adhiere a la esfera y esta la arrastra distorsionando la estructura que la rodea. Del mismo modo la rotación de la Tierra o de cualquier otro cuerpo, debería producir -según la relatividad general- un arrastre de la estructura geométrica que su propia masa genera al curvar el espacio-tiempo. Este tipo de efecto no está previsto en el modelo newtoniano para la interacción gravitatoria, y es de claro origen relativista. Ciertamente, en la teoría de Newton la fuerza gravítatoria sólo depende de la distancia entre los cuerpos que se atraen, sin importar si estos se mueven o no. En este sentido la gravitación de Einstein se comporta como el electromagnetismo de Maxwell, en el cual la carga eléctrica genera campo eléctrico, y el movimiento de la carga eléctrica genera campo magnético. El efecto es entonces el reflejo de la componente “magnética” de la gravedad relativista, y fue derivado por Joseph Lense y Hans Thirring en 1918. Para observar este efecto, podemos pensar que, así como el espín de una carga eléctrica “precede” en presencia de un campo magnético (es decir, la “rotación intrínseca” se balancea alrededor de la dirección del campo magnético, tal como el eje de un trompo lo hace alrededor de la vertical), la componente “magnética” de la gravedad relativista podría detectarse por sus efectos sobre el momento angular de un cuerpo.
Hasta 1997 este “gravitomagnetismo” no había sido nunca detectado experimentalmente. En ese año se produjeron dos novedades en el tema. Por un lado, Wei Cui (MIT), 5. N. Zhang (NASA) y Wan Chen (Univ. de Maryland y NASA) anunciaron la observación de la precesión del disco de acreción de materia en sistemas binarios que contendrían un agujero negro rotante. En tales sistemas binarios, una estrella normal orbita alrededor del agujero negro. El enorme campo gravitatorio del agujero negro succiona materia de la estrella, la que cae formando un torbellino en forma de disco. En este proceso, la materia en el disco se comprime, se calienta y emite radiación, especialmente en forma de rayos X. Estas emisiones fueron detectadas por el satélite RXTE (Rossi X-ray Timming Explorer) de la NASA. Los científicos observaron una modulación cuasi-periódica en el espectro de los rayos X en varios sistemas binarios con candidatos a agujeros negros, que interpretaron como debida a la precesión del disco de acreción provocada por la rotación del agujero negro.
Por otro lado, el equipo dirigido por Ignazio Ciufoliní (Universidad de Roma “La Sapienza”) anunció la verificación experimental del efecto Lense-Thirring producido por la rotación de la Tierra actuando sobre la órbita de un satélite artificial. En este caso, la precesión que se observó es la del momento angular orbital del satélite, lo que significa que lo que precede es la orientación del plano de la órbita. Si la Tierra no rotara, el plano de la órbita seria siempre el mismo (suponiendo una Tierra esféncamente simétrica). Pero el arrastre del espacio-tiempo producido por la rotación terrestre modifica permanentemente la orientación del plano orbital. La orientación de la órbita se determina por la ubicación de los puntos nodales -los puntos donde la órbita del satélite cruza el plano ecuatorial terrestre-, tal como lo muestra la figura 1. De acuerdo con la relatividad general, los puntos nodales de un satélite orbitando a 5800km de altura como el caso del satélite estudiado- deberían correr-se por causa de este efecto unos 2 metros por año (31 milisegundos de arco por año). Para observar un efecto tan débil, se requieren determinaciones muy precisas de la posición del satélite y un conocimiento detallado de la distribución de la masa de nuestro planeta, pues una distribución no esférica produce también (aun cuando el planeta no rote) un desplazamiento de los puntos nodales.
El experimento fue posible gracias a la existencia del sistema LAGEOS (Laser Geodynamics Satellite), diseñado originalmente para: 1) detectar desplazamientos de masa en la corteza terrestre -de utilidad en el pronóstico de terremotos-, y en los mares y en la atmósfera, 2) observar variaciones en la duración del día y movimiento de los polos, y 3) recoger todo tipo de información sobre la forma de la Tierra y su campo gravitatorio. Los satélites LAGEOS I (1976) y II (1992), construidos por la NASA y la Agencia Espacial Italiana (ASI) respectivamente, son dos esferas gemelas de 60cm de diámetro y de unos 400kg de peso. Están compuestos por dos hemisferios de aluminio unidos por un cilindro de bronce y cubiertos por 426 prismas reflectores (figura 2).Orbitan a alturas de 5.860km y 5.620km (perigeos) con poca excentricidad. Una red mundial, en la que cooperan más de 30 paises, rastrea desde Tierra las posiciones de los satélites mediante el envio de pulsos láser que son reflejados por los prismas. Puede afirmarse que estos satélites son los objetos en el cielo cuya posición conocemos con mayor exactitud, pues el error está por debajo de 1cm.
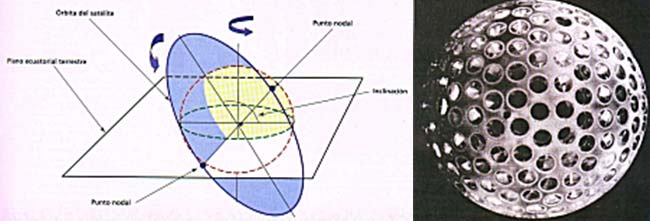Izq: Figura 1. Puntos nodales de la órbita de un satelite. Der: Figura 2.Imagen del satélite LAGEOS
Para medir el efecto Lense-Thirring se utilizó un programa que calcula la órbita de los satélites usando la teoría de la relatividad general y se tomó en cuenta el conocimiento actual acerca de la distribución de masa de la Tierra (apartamientos de la esfericidad, inhomogeneidades, mareas, etc.) -información recogida por el propio LAGEOS II-. El efecto Lense-Thirring entra en este cálculo con un parámetro asociado [cuyo valor es 1 para la Relatividad General. El experimento consiste en comparar los valores observados de los desplazamientos de los nodos y del perigeo, con los que resultan del cálculo con distintos valores de [, para ver cuál es el valor que mejor se ajusta a la observación. Utilizando datos recogidos durante tres años el valor cotenido para [fue 1,1 (Con un margen de error de un 25%, según la estimación de los autores). Esta seria la primera determinación experimental del efecto Lense-Thirring.
Aunque el resultado es auspicioso, fue recibido con cierta cautela por la comunidad científica, debido a que la estimación de errores ha suscitado controversias. La principal fuente de equivocación en este experimento proviene de los errores en la medición de los “momentos multipolares”. Estos son cantidades que caracterizan la falta de esfericidad de la distribución de la masa terrestre y por lo tanto, intervienen en el cálculo del campo gravitatono de la Tierra. No sólo no se los conoce con la precisión necesaria para este tipo de experimento, sino que son afectados por variaciones temporales difícilmente modelables. Sin embargo, los autores del experimento arguyen que han medido tres cantidades: los desplazamientos nodales de LAGEOS I y II, y el desplazamiento del perigeo de LAGEOS II (el del LAGEOS I es ínfimo debido a la casi nula excentricidad de su órbita), las cuales alcanzan no sólo para determinar [ sino también para resolver las incertidumbres en los primeros momentos multipolares pares J2 y J4-los momentos pares son los únicos que contribuyen al desplazamiento de nodos, y los momentos de orden más alto no lo hacen significativamente. No obstante, Clifford M. Will (Washington University) ha señalado que la medición del desplazamiento del perigeo es poco confiable porque, por un lado, está afectada por un error demasiado grande y, por el otro, está influida por los momentos multipolares impares. Otras fuentes de error son las perturbaciones no gravitatorias a la órbita debidas a la presión de radiación solar, y la absorción y reemisión anisótropa de la radiación infrarroja terrestre.
Con el propósito de disminuir la fuente de error más importante, se decidió el lanzamiento de un tercer satélite gemelo: LAGEOS III. En el nuevo proyecto colaboran Alemania, España, Estados Unidos, Francia, Gran Bretaña e Italia. La órbita de LAGEOS III tiene una inclinación suplementaria a la de LAGEOS I. Así se consigue que ambos satélites puedan verse como un único sístema en precesión que no es efectado do por J2 (la contribución de J2 a la precesión es proporcional al coseno de la inclinación de la órbita. Como las inclinaciones son suplementarias, entonces las contribuciones de J2 a las precesiones de cada satélite tienen signos opuestos, y la bisectriz del ángulo formado por las lineas de nodos de ambos satélites precede sin ser afectada por J2). Ciufolini considera que se podrá alcanzar un margen de error del 3% en la determinación del arrastre del espacio-tiempo. De confirmarse este resultado, sería esta la primera observación de los efectos gravitomagnéticos de la relatividad general, la que se sumará a las numerosas pruebas que ya cuenta la teoría creada por Einstein hace más de ochenta años.
