Cuando el cerebro inventa cosas
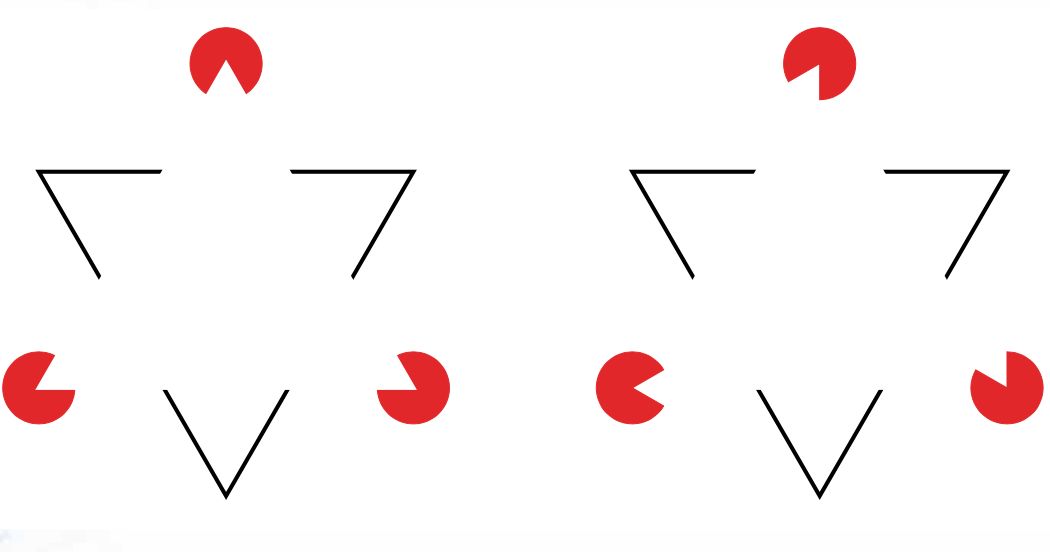
Mirá la imagen de abajo: ¿cuántos triángulos y círculos podés ver? ¿Y si ahora mirás la imagen de la derecha?
No todo lo que percibimos es real. En realidad, en ambas imágenes solo hay 3 Pac-Mans y 3 ángulos. La disposición de los Pac-Mans en la imagen de la izquierda confunde a nuestro sistema nervioso y le hace creer que hay un triángulo invertido con bordes negro (semioculto), 3 círculos rojos y, sobre ellos, un triángulo blanco superpuesto. La ilusión desaparece si disponemos de manera diferente los Pac-Mans, como en la imagen de la derecha. Esta famosa ilusión, conocida como triángulo de Kanizsa, pone en evidencia el fenómeno de relleno visual.
Si bien los mecanismos fisiológicos que subyacen al relleno visual (en este caso, la percepción de contornos que no existen) no se comprenden del todo, se acepta que el sistema nervioso rechaza la posibilidad de que las figuras se acomoden de tal manera como en la figura de la izquierda por mera ‘coincidencia’, ponderando como más probable que se deba a superposición de figuras. La ilusión es tan potente que se pueden percibir sutilmente contornos en el triángulo que apunta hacia arriba, cuando en realidad esos contornos no existen. Por otra parte, las imágenes en la retina son planas (en dos dimensiones); el procesamiento de dicha información a nivel de la corteza visual construye una imagen percibida que tenga sentido para el organismo: de esta manera, la imagen que percibimos parece ser una superposición espacial (en tres dimensiones) de varias figuras.
Comprando infinitos caramelos
En la edición anterior dedicamos unas líneas para debatir sobre la paridad del cero. Este número no tiene puntos medios: o hace todo muy fácil o lo complica hasta, incluso, hacerlo imposible. Por ejemplo, resulta muy fácil sumar cero, restar cero o multiplicar por cero. Pero si hay algo que quizá muchos recordamos de la escuela es que ‘no se puede dividir por cero’. Pero ¿por qué no se puede? ¿Qué quiere decir esto?
Para entender cuál es el problema, imaginemos que vamos a un kiosco con 100 pesos para comprar caramelos. Si cada caramelo costara 100 pesos, entonces solamente podríamos comprar 1. Pero si cada uno costara 50, podríamos comprar 2, y si el precio de cada caramelo fuera de 1 peso, nos alcanzaría para comprar 100.
Para saber cuántos caramelos podemos comprar, la cuenta es muy simple: hacemos 100 dividido el precio unitario, y el resultado es la cantidad de caramelos que podemos llevarnos. De esta forma seguimos: ¿cuántos caramelos podemos comprar si costaran 0,50? ¿Y si costaran 0,10? Pongamos los datos en una tabla para verlos mejor.
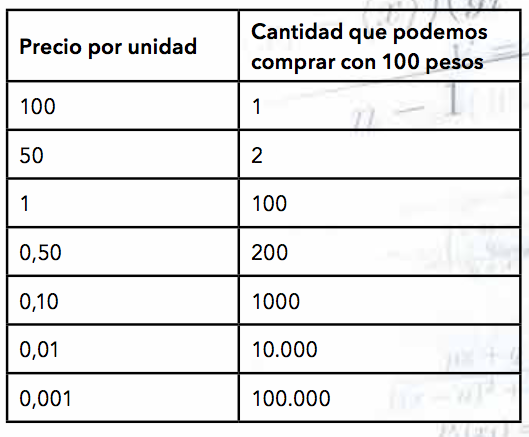
Y así podemos seguir, y resulta claro que mientras más barato sea cada caramelo, más cantidad podremos comprar con nuestros 100 pesos. Es decir, a medida que el precio disminuye, la cantidad de caramelos que podemos comprar aumenta. Imaginemos que el precio disminuye de a poco hasta llegar a cero. Entonces, ¿qué ocurre si el precio de cada caramelo es 0 pesos? Claramente podríamos llevarnos todos los caramelos del kiosco, sin importar cuántos haya. Si tuviera infinitos caramelos, podríamos comprarlos con nuestros 100 pesos, o con cualquier billete que tengamos en el bolsillo (pero ¡ojo!, no pretendamos estafar al comercio con un billete de cero pesos, la división de 0 entre 0 es otro debate).
Lo anterior nos dice que si dividimos un número cualquiera (que no sea cero) por cero el resultado es un valor tan grande como se quiera. Para indicar este valor se utiliza el símbolo infinito (que no es un número). Así, decimos que el resultado de dividir cualquier número no nulo por cero es infinito.
¿Qué pasará si queremos hacer cero dividido cero? Daremos la respuesta en el próximo número, pero invitamos a que vayan conjeturando el resultado…
#TeRegaloUnTeorema
Conjetura de Kepler (1611)
No hay mejor forma de acomodar las naranjas que como lo hace el verdulero.
Kepler publicó esta conjetura en 1611 en un librito llamado De niue sexangula, algo así como El copo de nieve hexagonal.
En matemática copetuda se dice así: ningún empaquetamiento de esferas tridimensionales congruentes tiene densidad mayor que las caras centradas (la de la foto).


El problema consiste en averiguar cuál es la mejor forma de acomodar las naranjas para que ocupen el menor espacio posible. O, dicho al revés, de meter la mayor cantidad de naranjas por unidad de volumen.
La forma de medirlo es con el porcentaje de volumen ocupado por las naranjas. Con la propuesta de Kepler da π/√18. Aproximadamente 74%.
El problema en sí ya es superinteresante si se tratara tan solo de naranjas, pero también es superimportante en mecánica estadística, un área de la física dedicada a entender las propiedades macroscópicas de la materia (gases, líquidos, sólidos) a partir de las interacciones microscópicas de las moléculas que la forman.
En ese marco es muy importante conocer cuáles son los estados de mínima energía. ¿Cómo deben acomodarse un montón de moléculas redondas (ponele) para minimizar la energía? Es muy importante saber si la forma en que deben hacerlo es en un arreglo ordenado, como el que conjeturaba Kepler, o en uno desordenado.
Este tipo de preguntas están en el centro de la investigación de Giorgio Parisi, uno de los recientemente laureados con un premio Nobel. Una prueba de la conjetura fue anunciada en 1998 (¡sí! recién en 1998) por Samuel Ferguson y Thomas Hales, pero no fue publicada hasta 2006 porque los referís encargados de revisar que la prueba fuera correcta no lograban dar un veredicto.
¡Y no lo lograron! Pero dijeron que estaban 99% seguros de que estaba bien.
La prueba consiste en reducir el problema a chequear muuuchas cuentas en una gran cantidad de casos. Esta última tarea es realizada con computadoras.
Por eso su prueba consistía de 300 páginas de notas y 3 gigabytes de programas de computadora, datos y resultados.
En 2003 Hales anunció Flyspeck, un proyecto para dar una prueba formal de la conjetura (una prueba que puede ser chequeada también usando computadoras). Estimó que el proyecto llevaría aproximadamente veinte años.
En enero de 2015, Hales y veintiún colaboradores subieron el artículo ‘A formal proof of the Kepler conjecture’ a arXiv, una plataforma donde (casi) todos los matemáticos subimos nuestros artículos apenas terminados: https://arxiv.org/pdf/1501.02155.pdf
Todavía no se conoce una prueba ‘libre de computadoras’ de la conjetura de Kepler. El gran John Conway creía que eso pasará algún día, aunque tal vez haya que esperar otros cuatrocientos años.
#TeRegaloUnTeorema
Matemática abstracta
En esta historia, como en el relato de Jorge Luis Borges ‘Emma Zunz’, hay un par de nombres propios mal, pero son de lugares y no de personas. Y los hechos son correctos, no hay que forzar la interpretación, se pueden rastrear y confirmar uno por uno.
Es la historia de un matemático de Australia, o Nueva Zelanda. O tal vez de otro lado, pero apostaría a que era de ahí. De Fiji no, ni de Sumatra, ni de Borneo: me acordaría por el TEG. Lo cierto es que hizo el doctorado en UCLA, California, y luego un posdoc en Harvard. ¿O era al revés? ¿Tal vez en Princeton?
No nos detengamos en esos detalles: cruzó el mundo de sur a norte, de este a oeste, y terminó trabajando en biología matemática. Consiguió un cargo en Canadá, como para cambiar también de temperatura, y se cambió el apellido: si no me creen, lo pueden guglear: se llamaba Smith (correctora, coincido que guglear no es un verbo castellano, pero qué le vamos a hacer, es lo que harán los que les pique el bichito de la curiosidad).
No recuerdo el nombre, los nombres son demasiado comunes, pero, con Smith y las pistas que les di, lo van a encontrar. Ah, perdón, ya me olvidaba: se cambió el apellido y ahora es Smith? No les estoy preguntando nada, le agregó el ? al apellido. Y si se preguntaban si le faltaba cambiar algo más, pues sí: cambió de género, así que también su nombre ahora es otro.
Y, como no podía ser de otra manera, cambió de tema de investigación.
¿Por qué?, se preguntarán. Bueno, lo cuenta en el prólogo de un libro, o en una entrevista: en algún momento del posdoc, o tratando de conseguir un cargo, se encontró en las cataratas del Niágara cazando mosquitos infectados con la fiebre del Nilo, y cazando mosquitos infectados con la fiebre del Nilo se dio cuenta de algo muy loco: los mosquitos estaban infectados con la fiebre del Nilo. Y eso es muy peligroso.
Entonces pensó en dedicarse a problemas abstractos, esos que todo matemático serio estudia con orgullo: álgebras de Lie, ecuaciones diferenciales no lineales –como el p laplaciano, acá yo levanto la mano–, topología algebraica, análisis harmónico… (correctora: el Diccionario enciclopédico Espasa Calpe de 1924 en 40 tomos o más que leía de chico le ponía h, y agréguele la deformación profesional de años de amistad con Fourier. Qué le vamos a hacer, me quedó esa mala costumbre, no se me ponga mal).
Vayan a guglear, y les puede costar encontrarlo, pero les doy una pista: agreguen zombies y ya está, van a saber de quién hablo, porque escribió un libro muy completo sobre cómo modelar epidemias… de zombies. Hay distintas herramientas matemáticas: ecuaciones diferenciales, estadística, simulaciones, de todo! Acá sí va el !, y no abrí el ¡, porque no sé bien a qué altura de todo el texto anterior comienza mi asombro, puede que antes del título.
Y van a coincidir que, como problema abstracto, lo que se dice abstracto, le gana de lejos a todos los que normalmente estudiamos.
Agua pa’l mate
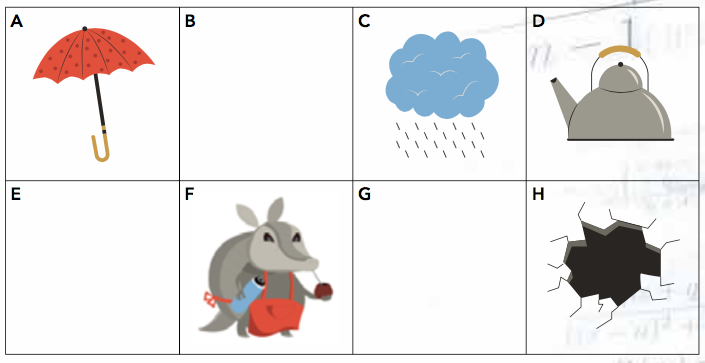
A Lita la mulita se le terminó el agua y tenía ganas de tomar unos mates, por lo que tiene que ir a buscarla a la pava.
El camino está lleno de obstáculos y objetos que Lita puede recoger y usar. Se sabe varias cosas sobre Lita:
• No le gusta mojarse.
• No le gusta caerse a un pozo.
• Sabe usar paraguas.
• Si hay, le gusta comer facturas con el mate.
• Se puede mover para arriba, abajo, izquierda y derecha (➡⬆⬇⬅) y juntar y usar cosas.
Ahora bien, es fácil ver que el recorrido que le conviene a Lita es ⬅⬆ ➡➡➡.
Con el primero se mueve a la celda E, después levanta el paraguas y avanza por la lluvia sin mojarse.
Ahora bien, todo esto lo pudimos decir porque tenemos un gran conocimiento de los objetos presentes y de la situación que queremos resolver. Pero ¿qué pasaría si Lita no supiera nada del mundo y tuviera que explorarlo por primera vez?
Este es el ejercicio que nos proponemos. Estudiar el mundo y generar un conocimiento sobre lo vivido para que Lita pueda, con este conocimiento, recorrer el plano y conseguir el objetivo: tomar mate.
Para ello vamos a plantear algunas reglas:
• Llegar a la pava significa lograrlo, a lo cual le asignaremos un puntaje alto: 100.
• Pasar por la lluvia sin paraguas nos moja y perdemos -50 puntos.
• Caernos al pozo también nos hace perder -50 puntos.
• Lita puede tener dos estados: con paraguas o sin paraguas.
Ahora vamos a ver cómo Lita empieza a conocer el ambiente. A cada paso que tiene que dar tiene dos opciones: explorar algo nuevo al azar o usar conocimiento previo para avanzar.
Como la primera vez no tenemos conocimiento, entonces vamos a hacerlo al azar hasta que gane o pierda muchas veces:
Corrida 1:
➡ ⬅➡ ⬅➡ ⬆ de esta manera recorre las posiciones F (inicial) GFGFGC y se moja y pierde, por lo que recordará que toda esta secuencia fue mala.
Vamos a hacer una segunda corrida. Ahora Lita ya sabe que, en su corta experiencia, ir a la derecha le hizo perder.
⬆ ⬅➡ ➡ ⬅➡ ➡ de esta manera recorre las posiciones F (inicial) BABCBCD y llega hasta la pava ganando 100 puntos, así que recordará esta secuencia como buena.
En una tercera corrida:
➡ ➡ de esta manera recorre las posiciones FGH y pierde porque se cae al pozo.
Luego de muchas corridas, Lita logró hacer una composición de qué hacer en cada situación de acuerdo con su experiencia.
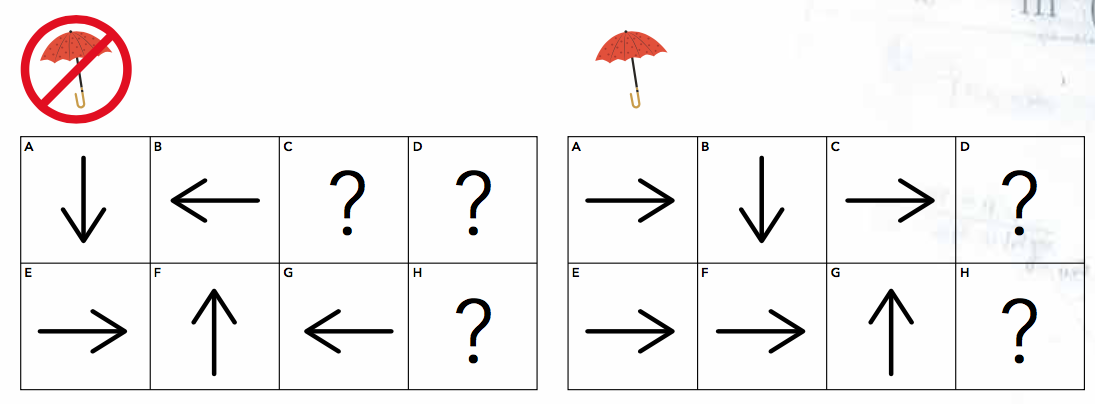
Política (el plan de Lita): qué hacer en cada casilla
Esto es lo que vamos a llamar una política, es la definición de qué va a hacer Lita si se encuentra en cada una de las celdas separadas en dos situaciones: sin paraguas (izquierda), con paraguas (derecha). Las casillas indicadas con ? indican que Lita no sabe qué hacer si se llega a encontrar en esa posición (sea porque nunca pasó o porque gana o pierde y no tiene acción posible).
La pregunta ahora es la siguiente: con este conocimiento, ¿puede Lita asegurarse de llegar siempre a la pava en este escenario?
¿Qué pasaría si, además de estar el paraguas, el escenario contara con unas medialunas que a Lita le encantan en la celda E? En este caso, en lugar de tener dos políticas, Lita deberá tener cuatro posibles: sin objetos, con medialunas (1 objeto), con paraguas (1 objeto) o con paraguas y medialunas (2 objetos). ¿Te animás a planificar una política para este nuevo escenario?
Corolario
Esta nueva forma de aprender de Lita se denomina aprendizaje por refuerzo, y es una rama de machine learning (que es a su vez parte de la inteligencia artificial). En el aprendizaje por refuerzo se busca resolver problemas planteados como ‘caminos’ (que podrían no ser tan literalmente caminos) y gracias al algoritmo ejemplificado aquí por Lita se pueden mediante exploración (y obtención de recompensas por acciones) encontrar soluciones a problemas muy grandes y complejos que no pueden ser resueltos (o al menos no tan rápidamente) con algoritmos normales.
Para leer más: es.wikipedia.org/wiki/Aprendizaje_por_refuerzo
Soluciones
Agua pa’l mate
Como ya podrá arriesgar, Lita sí llega. Y veamos cómo. Lita parte sin paraguas de F, por lo que tiene que ir para arriba (ver política mapa izquierdo), desplazándose a B, ahí la estrategia es ir a la izquierda, llegando a A y tomando el paraguas. Ahora Lita tiene el paraguas, por lo que debe seguir el plan del lado derecho, lo cual la lleva de A por BFGC hasta D llegando a la pava.
Equipo de la sección ‘Ilusiones y juegos matemáticos’
Marilina Carena
Matemática, UNL-Conicet.
[email protected]
Nicolás Fernández Larrosa
Biólogo, IFIBYNE, UBA-Conicet.
[email protected]
Pablo Groisman
Matemático, UBA-Conicet.
[email protected]
Matías López-Rosenfeld
Computador, UBA-Conicet
[email protected]
Juan Pablo Pinasco
Matemático, UBA-Conicet.
[email protected]
Nicolás Pírez (coordinador)
Neurobiólogo, IFIBYNE, UBA-Conicet.
[email protected]
Alfredo Sanzo
Ingeniero, ICC, UBA-Conicet.
[email protected]
Nicolás Sirolli
Matemático, UBA-Conicet.
[email protected]
Preguntas, comentarios y sugerencias: [email protected]











