Ciencia, pasión de multitudes
Recuerdo mi infancia, allá en los años 60, cuando los progres de aquel entonces (mis padres entre ellos) sus-piraban amargamente mientras repetían cual mantra ‘¡qué barbaridad que un tipo gane mucha más plata por pegarle a una pelota que por lograr un adelanto científico!’.
Digamos que hacían una comparación muy poco cientí-fica entre los futbolistas, y valga la redondancia (de la pelota), los hombres de ciencia. En general la cosa quedaba zanjada cuando algún aguafiestas les preguntaba cuánta gente pagaría una entrada por ver a un microbiólogo persiguiendo a una bacteria en el área penal. ‘Cínico, pero tristemente cierto’, decía el coro de amigos, y ya.
Pero, dicen por ahí, el fútbol siempre da revancha.
Y de hecho, poco menos de sesenta años más tarde, en este 2020 coronático y febril, nos encontramos con los científicos en la tapa de los diarios, y el fútbol, en gran parte del planeta, suspendido hasta que… justamente, los científicos metan el golazo a nivel vacunatorio o farmacológico que permita a miles de millones de seres humanos encontrar el sentido de sus vidas para el domingo a la tarde, quizá extensible al resto de la semana.
Cierto que en algunos países ya se reanudó, pero todo está pendiente de un pequeño ser, ni siquiera un ser vivo, invisible y cruel, que nos tiene a todos formando la barrera en nuestras propias casas, y, en muchos casos, apasionados hinchas de Boca, River o San Lorenzo a duras penas sostenidos emocionalmente por algún partido de Suiza, Burkina Faso o Laos.
Quiero decir, hay millones de argentinos que se bancan más de siete meses sin laburo, sin sexo, sin asado, sin picada con amigos, sin cafecitos, pero ¿¿¿sin fútbol???
Son esos los que, cada vez que un infectólogo aparece en la tele, en vez de preguntar: ‘¿Qué dijo sobre la cuaren-tena?’, pregunta: ‘Che, el micróbiólogo ese ¿será de Boca, de River, de Talleres?’.
Quizá sea el momento en que la ciencia deba op-tar por la grandeza, olvidarse de viejos ninguneos y pos-tergaciones económicas, y hacer el esfuerzo necesario para que pueda volver el fútbol y la gente a las canchas.
Porque, si no, va a estar difícil.
Quiero decir, es muy difícil imaginarse un partido en tiempos de pandemia. Podríamos pensar en un partido donde estén los veintidós con barbijo (el de cada equipo con sus colores), que además podrían ser aprovechados por empresas fabricantes de lavandinas o alcohol en gel para esponsorearlos, y así aliviar la difícil situación de los clubes.
Ahora bien, si un jugador le saca el barbijo a otro, ¿es penal, corresponde tarjeta roja, o que el árbitro le eche un chorro de lavandina?
¿Deben cambiarse los botines e incluso las camisetas cada vez que entran al área penal del equipo contrario?
El arquero ¿debe usar diferentes guantes descartables para cada atajada?
Dado el aislamiento social obligatorio, ¿cómo se hace para sacarle la pelota a un rival estando a un metro y medio de distancia?
¿Puede haber policías en la mitad del campo con-tro-lando que solo lo atraviesen los jugadores con permiso para hacerlo?
¿Hay que lavarse las manos y tomarse la temperatura cada vez que uno toca la pelota que ha sido tocada por un compañero o por un rival?
¿Y si, para evitar contagios, mejor cada equipo juega en su cancha, y el rival lo ve por Zoom?
¿Y si para ser más cuidadosos aun, cada jugador juega desde su casa y están todos comunicados por internet? ¿Se imaginan a Messi gambeteando a su celular?
El famoso cantito de la tribuna ‘¡Y ya lo ve, y ya lo ve, es para [otro equipo] que lo mira por tevé!’ no va a ser más una burla, sino un elogio a la buena conducta cívica del equipo así nombrado.
Cuando un jugador se acerca al arco contrario, nadie podrá gritarle al arquero: ‘¡Salí, salí!’; más bien, el director técnico debería gritar: ‘¡Quedate en casa, que de un gol en contra se vuelve, pero el virus es muy peligroso!’.
¿Vale gol de barbijo?, ¿y de máscara protectora?
Sin duda el esquema sería más defensivo; los jugadores solamente saldrían de su área cuando necesitasen comprar algo esencial en algún negocio de la cercanía.
Los delanteros podrían reclamar un subsidio porque solo pueden cometer el 30% de los goles que hacían antes. El Estado podría adjudicarles algunos goles a los más necesitados.
Darle un codazo a un rival, ¿es un foul, o un saludo?
¿Y si en medio de una jugada el que lleva la pelota es detenido por un defensor contrario que le cuenta el último capítulo de la serie de Netflix? ¿Se cobra foul o spoil?
Queridos científicos, como verán, esto es insostenible. Ayúdennos a terminar pronto con este coronamundo, así los jugadores vuelven a ganar fortunas, y los progres de ahora podemos volver a quejarnos de eso, no sin cierta envidia.
Rudy
Contraste: cómo se definen los límites de un objeto
Consigna. Te proponemos que observes la imagen. Veras una serie de barras azules. ¿Son iguales entre sí? Ahora te proponemos que tapes los límites entre las barras azules valiéndote de una tira de papel: ¿seguís pensando que son distintas?

Explicación. Incluso si observás bien, percibimos un degradé de azul dentro de cada barra. Ese degradé no existe en la imagen sino que es percibido. Tapá los dos bordes de una barra azul y notarás que no está. ¿Por qué ocurre esto? Durante el procesamiento visual, el sistema necesita detectar los límites de un objeto. Para ello, aumenta el contraste: aquello que es más claro, cuando limita con algo más oscuro, se vuelve más claro; mientras que lo oscuro, al lado de algo más claro, ¡se hace más oscuro! De esta manera, cuando se tapa el límite entre dos barras azules ya no es tan sencillo distinguir que las dos barras son de azules diferentes. De esta manera, nuestra percepción de los colores y de la intensidad lumínica es relativa al contexto.
#TeRegaloUnTeorema
Teorema de Bayes (O… por qué un test positivo y un infectado pueden ser cosas muy distintas)
Es uno de esos teoremas en los que el cociente entre la dificultad de su demostración y lo profundo de su enunciado + su impacto da casi cero. Tanto, que suele pasar que a primera vista no se comprende por qué lleva el mote de teorema.
Dice así: si A y B son dos eventos y llamamos P(A|B) a la probabilidad de que ocurra A, teniendo la info de que ocurrió B, entonces la probabilidad de que ocurra B, sabiendo que ocurrió A es la siguiente:
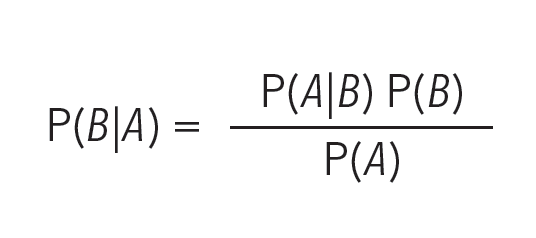
Y la demostración es facilísima una vez que nos convencemos de que P(B|A) = P(B y A) / P (A) porque entonces P(B y A) también es igual a P(A|B) P (B).
La cuestión es que este teorema, que acabamos de demostrar en un renglón, es muy profundo porque:
Nos enseña que se pueden calcular probabilidades a posteriori. No solo podemos fijar las condiciones de un experimento y calcular las probabilidades de los posibles resultados, sino que también podemos observar el resultado de un experimento y preguntarnos por las probabilidades de los posibles escenarios que lo generaron.
Eso suena a fundamental a la hora de querer inferir cuestiones a partir de observaciones, lo que hoy llamamos estadística. Bah, también lo llamamos machine learning, data science, big data y otros cuantos nombres más. Y en realidad dicho así es lo que hoy se llama estadística bayesiana y es solo un posible enfoque. Hay también otros enfoques y durante muchos años formaron juntos la gran grieta de la estadística, al lado de la cual la que tenemos en la Argentina es un poroto. Con grandes exponentes de ambos lados.
Nos enseña que P(B|A) y P(A|B) pueden ser muy distintas y no hay que confundirlas.
Por ejemplo, si queremos hacer un test serológico para detectar un anticuerpo determinado, y lo que queremos saber es si el test es posta o maso maso, nos interesa saber si un individuo al que el test le dio positivo realmente tiene el anticuerpo (o lo que sea que queramos testear) o al menos que la probabilidad de que eso pase sea alta. Llamemos
TP = test positivo, TN = test negativo, A = tiene anticuerpos, NA = no tiene anticuerpos.
La info que podemos tener es P(TP|A) (sensibilidad) y P(TN|NA) (especificidad) porque así se prueba el test, probándolo en gente que se sabe tiene (o no) los anticuerpos y viendo qué da. Pero lo que nos interesa es
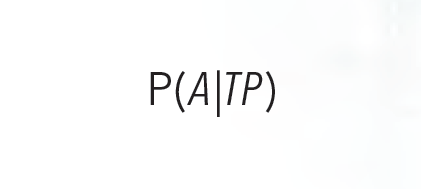
que, por el teorema de Bayes, lo podemos calcular haciendo

Hagamos un ejemplo. El Cellex qSARS-CoV-2 IgG/IgM Rapid Test, para detectar anticuerpos asociados al coronavirus, tiene una sensibilidad de 93,8% y una especificidad de 96,4% (www.fda.gov/media/136625/download).
Para hacer las cuentas necesitamos P(A). Eso es, si elegimos una persona al azar, qué probabilidad tiene de tener los anticuerpos. Se corresponde con el porcentaje de infectados en la población, que justamente no lo sabemos. Supongamos una población de 44 millones de habitantes con unos 130.000 casos confirmados. Podemos hacer cuentas conservadoras (o sea, exagerar) y asumir que la cantidad de infectados es 10 veces eso. Unos 1.300.000. Eso es aproximadamente el 3% de la población. O sea que P(A) = 0,03.
Con estos números podemos calcular P(TP) con una cuenta que se llama probabilidad total y que dice que

Es decir que cuando el test da positivo, la probabilidad de tener realmente los anticuerpos es cerca del 45%. ¡Y la de no tenerlos es 55%!
Esto pasa porque, al menos por ahora, la prevalencia parece ser P (A) muy baja. El hecho de saber que a alguien el test le dio positivo hace que aumente mucho su probabilidad de tener los anticuerpos (¡se multiplicó por 10!, el test hizo bien su trabajo), pero sigue siendo baja.
¡Así que ojo! Una cosa es P(TP|A) y otra muy distinta es P(A|TP).
Bajando el R0 (en la ruleta)
Le proponemos al lector que nos acompañe al casino. Más precisamente, a jugar a la ruleta.
Si apostamos todas nuestras fichas a un color (rojo o negro) y somos favorecidos por el azar al caer la bola en un número de ese color, el casino nos pagará dos veces lo que hayamos apostado.
Esto da lugar a una estrategia, bien conocida, que consiste en seguir este algoritmo:

Empecemos por las buenas noticias: cuando salga rojo, la ganancia será tal que recuperaremos todas las fichas que perdimos en las jugadas previas, en las que salió negro, y nos quedará una ficha a favor. Por ejemplo, supongamos que empezamos jugando una ficha al negro, y que salió rojo recién en la quinta jugada. Entonces:

Esto no es particular de haber ganado en la quinta jugada; es totalmente general, y no es difícil de demostrar, recurriendo a fórmulas para la suma (geométrica) que nos da la cantidad total invertida en la enésima jugada.
Siguiendo, es poco probable que tengamos que esperar mucho hasta que salga rojo. Esta probabilidad se mide con un número que está entre 0 (poco probable) y 1 (muy probable). La probabilidad de que salga negro en una jugada es ½. Así, la probabilidad de que salga negro cinco veces seguidas, asumiendo que el croupier no se disguste con nuestra estrategia y empiece a apuntarle al negro, es ½ * ½ * ½ * ½ * ½, que decimalmente es 0,03125. Yendo más lejos, la probabilidad de que salga cien veces seguidas es igual a
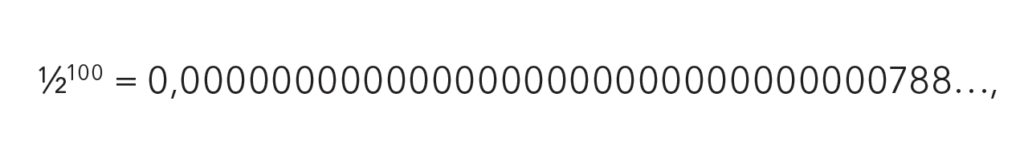
lo cual nos invita a confiar en que, si el azar y el croupier no se ensañan con nosotros, a la larga saldremos victoriosos.
Abordemos las malas noticias. Para empezar, aunque sea muy poco probable, la ruleta podría arrojar negro indefinidamente, dejando a nuestro algoritmo en un bucle infinito. Siguiendo, además del rojo y el negro, la ruleta tiene un número de color verde: el cero. Con lo cual, en verdad, la probabilidad de perder en una jugada es más alta que lo que consignamos: es igual a 19 / 37, o sea 0,5135…
Digresión: si bien podría parecer que esto se salva jugando, en lugar de rojo contra negro, a par contra impar, para la ruleta el 0 no es par ni impar, contrario a lo que afirmamos los matemáticos.
Pero el problema en que queremos enfocarnos es el siguiente. La cantidad de fichas que hay que invertir crece muy rápidamente. Es un crecimiento exponencial, cuya base, dado que duplicamos en cada jugada lo apostado en la jugada anterior, es igual a 2. Más precisamente, la cantidad de fichas que hay que apostar en la enésima jugada es igual a 2n (y esto no tiene en cuenta lo perdido en las anteriores). Por ejemplo, si cada ficha vale 1 peso, en la jugada número 42 deberíamos apostar, al día de hoy, todas las reservas del BCRA.
Digresión: además de estos problemas, consignemos que el casino pone topes máximos al monto a apostar. Topes que este humilde jugador nunca llegará a ver ni de lejos, quedando sus arcas exhaustas muy tempranamente.
De tanto escuchar la voz de los epidemiólogos en estos tiempos, nos proponemos bajar el R0. Más precisamente, dar una estrategia en la que el monto a apostar crezca más lentamente con el correr de la mala suerte. Aun siendo exponencial, si logramos que el crecimiento tenga una base menor que 2, estaremos ante un mejor escenario.
La ruleta también tiene divididos a sus números en tres docenas (quedando el 0 excluido de ellas). Nos pagará el triple de lo apostado si acertamos la docena. Elegimos una docena, digamos la primera, y proponemos la siguiente variación de la estrategia original:
En la primera jugada apostar una ficha, y (si perdemos) en la segunda también.
Mientras no hayamos ganado, apostar en cada jugada la suma de lo apostado en las dos jugadas anteriores.
Por ejemplo, si acertamos a la docena recién en la quinta jugada, habremos:
invertido 1 + 1 + 2 + 3 + 5 = 12 fichas
ganado 3 * 5 = 15 fichas
lo cual nos deja un balance positivo. Como antes, esto no es particular de la quinta jugada; se puede demostrar que el balance será siempre positivo.
La cantidad de fichas que vamos apostando es bien conocida: conforma la sucesión de Fibonacci. La buena noticia es que esta crece más lentamente que la anterior. Más precisamente, se puede demostrar que el monto a apostar en la enésima jugada, es decir el enésimo número de Fibonacci, es aproximadamente igual a φn / √5, siendo
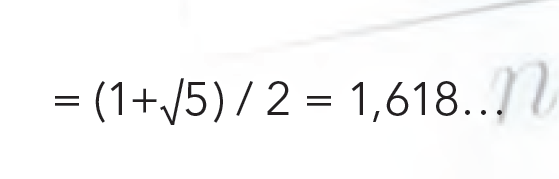
el número de oro, no solo presente en el arte sino, como vemos, también en la timba.
En limpio, el crecimiento sigue siendo exponencial, pero con una base bastante menor que 2. Esto nos permitirá jugar durante más tiempo: por ejemplo, habremos vaciado las arcas del BCRA recién luego de 62 jugadas desafortunadas. Pero necesitaremos más suerte para ser exitosos: acertar a la docena es más difícil que acertar el color. Por ejemplo, la probabilidad de perder cien veces seguidas es mayor que antes: es igual a
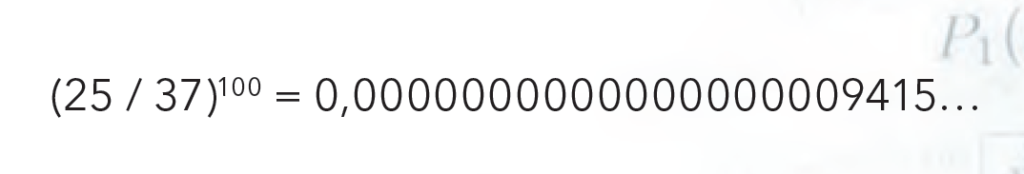
Todo no se puede.
Páginas de un libro, páginas de internet
Ponele que tenés un libro (de los antigüitos, de papel) con más o menos 1.000 páginas, y te olvidaste de ponerle un marcador, o de doblar la puntita de la página en la que te quedaste (ay, me duele un poquito cuando la gente hace eso, aunque confieso que alguna vez lo he probado). Pero tu memoria es prodigiosa: la página a la que querés llegar es la 613. La pregunta es: ¿cuántas páginas abrís como mínimo hasta llegar a la 613? Pista: ¿abrís en el medio (ponele, página 588) y vas pasando una por una, o hay una mejor forma?
Corolario
¿Cómo hace Google para encontrar la página entre millo-nes de millones de páginas que tiene el vasto libro de la interné? ¡No hay compu suficientemente rápida para ir pasando una a una todas esas páginas! ¿Y si lo que yo buscaba estaba en la última? Google usa lo que se llama un índice ¡como el de los libros!, y para buscar cosas dentro de ese índice, ¡que pesa miles de miles de gigabytes!, hace muy parecido a como vos hiciste para encontrar tu página rápidamente. Utilizando una estrategia, un algoritmo, que no es el de ir abriendo una por una, sino que hay un truquito. ¿Cuál es el tuyo?
Más información: elgatoylacaja.com.ar/destripando-google
Solución
Páginas de un libro, páginas de internet
Abro más o menos a la mitad, y me fijo: ¿le pegué a la página 613? Si no le pegué (y abrí en la 588, por ejemplo), abro a la mitad el cachito de libro a la derecha, y así voy abriendo a la mitad de cada nuevo cachito hasta encontrar la página 613. Con esta forma tenemos la seguridad de que con 10 pasos ¡o menos! llegamos con seguridad a cualquier página, no solo a la 613. ¿Por qué 10? Ese, querides lectores, es otro desafío.
Equipo de la sección ‘Matemática, ilusiones y humor’
Nicolás Fernández Larrosa
Biólogo, IFIBYNE, UBA-Conicet
[email protected]
Pablo Groisman
Matemático, UBA-Conicet
[email protected]
Juan Pablo Pinasco
Matemático, UBA-Conicet
[email protected]
Nicolás Pírez (coordinador)
Neurobiólogo, IFIBYNE, UBA-Conicet
[email protected]
Rudy
Humorista
[email protected]
Alfredo Sanzo
Ingeniero, ICC, UBA-Conicet
[email protected]
Nicolás Sirolli
Matemático, UBA-Conicet
[email protected]
Preguntas, comentarios y sugerencias: [email protected]











