Enmendando reglas
¿Cuántas veces nos encontramos acertijos en los que se da una lista finita de números ordenados y se pregunta cuál debería ser el siguiente? Se espera que el lector encuentre una regla a la que se ajustan los números dados y que, a partir de ella, se infiera cuál debería ser el número siguiente.
Este fue el tema que abordamos en el número anterior de la revista y concluimos que cualquier número puede ser el siguiente. ¿Qué significa esto? Quiere decir que uno podría elegir el valor que se le ocurra como candidato a ser el siguiente número y, luego, siempre se puede construir una regla que se ajuste a todos ellos. Veremos una de las tantas formas de encontrar una regla así. Para ello vamos a retomar el mismo ejemplo que presentamos en la edición anterior, ilustrado en la siguiente imagen.

En la mayoría de los casos en los que se plantea lo anterior se espera que la persona responda que el número siguiente en la lista es el 16, ya que en la posición de la misma se encuentra el número 2n (equivalentemente, cada número que aparece es el doble del anterior). Así, la regla 2n nos arroja la siguiente lista ordenada:
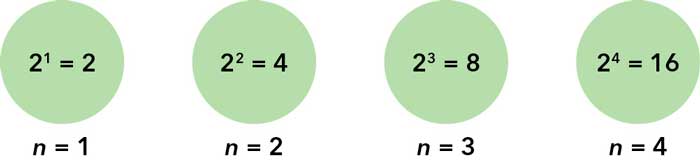
Pero vimos que esta no es la única regla que describe a los números dados por nuestro primer personaje de la escena, ya que también es cierto que en la posición n de la lista se encuentra el número n2 — n + 2. Según esta regla, el número que ocupa el cuarto lugar es, tal como afirmó el segundo personaje, el 14:

Pero ¿de dónde salió la fórmula n2 — n + 2? Más precisamente: dada una lista finita de números, ¿cómo podemos obtener una regla que se ajuste a todos? Por ejemplo, dada la lista 1, 3, 9, 27, 81, ¿cómo encuentro una regla para que el número siguiente sea 100, π, o lo que se me ocurra? Para explicarlo, volvamos a nuestro ejemplo.
Los números dados eran 2, 4 y 8 y, ahora, estamos agregando el 14 (porque quisimos, pero podría haber sido cualquier otro). Queremos, entonces, hallar una regla que se ajuste a estos cuatro valores ordenados así: 2, 4, 8, 14.
La forma de construir la regla que vamos a ver surge de los teoremas de interpolación polinómica. En cualquier texto sobre eso se pueden encontrar las fórmulas, pero quizá resultan medio complicadas a primera vista. En su lugar, construiremos recursivamente esta regla según la cantidad de datos a los que queremos ajustarla, y observaremos la idea que hay detrás para poder extenderla.
Supongamos, primero, que queremos obtener una regla de la que se infieran solo los dos primeros números: 2 y 4. Es fácil ver que la regla 2 + 2 (n — 1) lo cumple, pero el tercer número, el 8, ya no se ajusta a ella:

Pero ¿cómo y por qué elegimos esa regla inicial? ¿Qué ‘forma’ tiene? El primer término modela al primer valor, mientras que el segundo tiene dos características: una es que no ‘arruina’ el trabajo que ya hizo el primer término, pues se anula cuando n toma el valor 1 debido a la presencia del factor (n — 1). Esto hace que el primer elemento de la lista tome el valor 2, que es el término izquierdo de la fórmula. Por eso planteamos la regla con la forma
2 + x (n — 1),
donde solo falta determinar x de modo que la expresión anterior valga 4 cuando n = 2. Es decir, queremos que 4 = 2 + x (2 — 1).
Al resolver, se obtiene x = 2.
Así, hemos encontrado una regla que se ajusta bien a los dos primeros elementos de la lista pero vimos que, cuando n = 3, ya no arroja el tercer valor deseado, que era 8. ¿Cómo corregimos esto sin arruinar lo que ya logramos para los dos primeros valores? Aplicando el mismo razonamiento que antes: a la regla que obtuvimos le sumamos un término (llamado enmiendao corrector) que tenga dos características:
Característica 1 de la enmienda: debe anularse cuando vale n 1 y también cuando vale 2, para que no arruine el trabajo ya hecho para los dos primeros elementos. Esto lo logramos agregando los factores (n — 1) y (n — 2). Así, la nueva regla tendrá la forma siguiente:
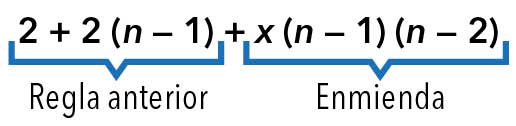
Característica 2 de la enmienda: que se ajuste al tercer elemento de la lista, es decir, que haga que la regla valga 8 cuando n = 3. Esto lo conseguimos eligiendo un valor adecuado para x. Al reemplazar esto en la regla, nos queda
8 = 2 + 2 (3 — 1) + x (3 — 1) (3 — 2)
Resolviendo un poco esta ecuación tenemos que 8 = 6 + 2x,
lo que arroja x = 1. Por lo tanto nuestra regla, hasta el momento, es 2 + 2 (n — 1) + (n — 1) (n — 2). Si operamos, podemos reescribirla como n2 — n + 2. Así, esta regla modela de forma correcta los tres primeros elementos de la lista y, de casualidad, también al cuarto (con n = 4 se obtiene 14). Entonces no debemos hacer un nuevo ajuste, y podemos afirmar que el número 14 puede ser el siguiente número en la lista 2, 4, 8, y exhibir la regla que respalda esto.
¿Qué hubiera pasado si, por ejemplo, quisiéramos imponer al número 38 como cuarto término? Deberíamos repetir el razonamiento para enmendarla sin arruinar lo hecho, por lo que en la enmienda agregamos los factores (n — 1) (n — 2) (n — 3), para no arruinar ahora los tres primeros valores que ya logramos ajustar. Para eso planteamos una nueva regla de la forma:
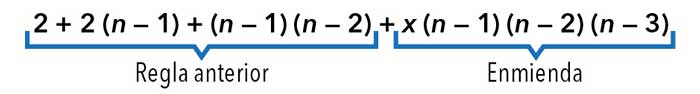
y determinamos el valor de de modo que la expresión valga 38 cuando n = 4, ajustando así la regla al cuarto valor de la lista:
38 = 2 + 2 (4 — 1) + (4 — 1) (4 — 2) + x (4 — 1) (4 — 2) (4 — 3),
de lo que obtiene x = 4. Así, la regla sería:
2 + 2 (n — 1) + (n — 1) (n — 2) + 4 (n — 1) (n — 2) (n — 3),
lo que se puede operar y reescribir como 4n3 — 23n2 + 43n — 22.
De esta forma se puede ir enmendando una regla de modo que coincida con una cantidad finita de números dados, y con cualquier otro que se nos ocurra agregar. Por supuesto que esta no es la única forma de construir una regla que cumpla con esto, pero es una de ellas.
Desafío: hallar la regla de modo que el número siguiente a la lista ordenada 2, 4, 8 sea 20.
Quisiera terminar mencionando que, seguramente, la respuesta ‘natural’ es que el número siguiente a la lista 2, 4, 8 sea el 16. Más ‘natural’ se vuelve la regla cuanto más larga es la lista que se muestra, si es que existe un consenso sobre lo ‘natural’. El objetivo de este texto es, simplemente, usar respuestas ‘no naturales’ como excusa para contar métodos de interpolación, que tampoco son el único camino de construcción de tales respuestas.
No hace falta enmendar reglas
1. Hay dos preguntas que los matemáticos suelen responder inmediatamente, y casi todos de forma muy similar:
Pregunta 1. ¿Qué número debería jugar a la lotería?
Respuesta 1. ¡No deberías jugar a la lotería nunca porque la esperanza matemática es negativa!
Pregunta 2. ¿Qué número continúa esta sucesión (inserte aquí alguna lista de números, por ejemplo 1, 3, 4, 6, 4, 6…)?
Respuesta 2. ¡Cualquiera! No tiene sentido esa pregunta, se puede interpolar una función (de hecho, infinitas) que en los primeros naturales valga exactamente la lista de números dada, por ejemplo 1, 3, 4, 6, 4, 6… pero que el siguiente sea cualquiera.
Voy a dejar el análisis de la primera para otra oportunidad, que no es cuestión de pelearme de golpe con todos mis colegas. Y tampoco me convence el rechazo a la segunda pregunta, en especial cuando se describe a la matemática como una ciencia que busca patrones.
2. Decía Henri Poincaré que un científico actúa como un chico que recorre una playa y analiza las piedras que encuentra. Le llaman la atención las más raras, conoce rápido aquellas muy repetidas, vería la frecuencia con la que aparecen los distintos tipos… pero no haría nada si todas las piedras fuesen distintas: ninguna le llamaría la atención al ser todas únicas. Y no tendríamos ciencia.
Poincaré se apoya en Tolstoi cuando habla de esto: si uno estudia los hechos, dado que hay infinitos hechos, lo importante es cuáles se seleccionan, y con qué criterios. Debe existir una jerarquía, y algunos serán más importantes que otros. De paso, Tolstoi descreía de la jerarquización que hacen los científicos modernos: se basa en caprichos por curiosidades inútiles, o mero utilitarismo, decía. El texto de Tolstoi arranca con una expresión en griego que podríamos traducir como ‘A cada argumento le podemos emparejar otro igual’, buen punto de partida para nuestro problema de las secuencias numéricas.
3. Tenemos una secuencia de números, nos preguntan cuál sigue, y podemos responder cualquiera. Hay infinitos números disponibles, y ninguno es preferible. Podríamos quedarnos inmóviles como el asno de Buridan, que enfrentado a dos fardos de pasto en direcciones opuestas muere de hambre al no decidirse por ninguno.
Jean Buridan, además de este dilema, nos dejó un gran consejo (ya que fue él quien formuló la navaja de Occam y no Occam): no multipliquemos los entes innecesariamente. En criollo, hacela fácil. Busquemos el patrón más sencillo que explique la secuencia. Y esa es la gracia de estos problemas: hallar la regla más simple que los explique.
Pero si a uno realmente le molestan estos problemas, la mejor revancha es encontrar una segunda regla, todavía más simple que la de la solución oficial. Créanme que en más de un problema se puede. A cada argumento que explique la secuencia, traten de emparejarle otro igual.
5. Para terminar, a Adrián Paenza no le gustaban estos problemas. Sin embargo, creo que el problema más lindo que podemos encontrar en sus libros, notas o programas de televisión es descubrir el número tachado en la siguiente secuencia: 06, 68, 88, X, 98…
Decía Paenza que los chicos coreanos de primaria podían resolverlo. Y los adultos, profesionales de mil disciplinas incluyendo doctores en matemáticas, no.
6. Esto sigue brevemente en las soluciones, pero primero intente con estas dos secuencias:
a) 06, 68, 88, X, 98… ¿cuál va en lugar de la X y por qué?
b) 1, 3, 4, 6, 4, 6… ¿cuál es el próximo entero y por qué?
El (infame) vestido
¿Es azul y negro? ¿O es blanco y dorado? Quien lo percibe de una forma, suele tener dificultad para concebir que alguien pueda verlo de la otra.
Pero ¿cómo es posible que una imagen estática genere una grieta en la opinión pública sobre algo tan básico como su color?
Este interrogante produjo una grieta análoga en la opinión científica, donde diferentes expertos proveyeron variadas explicaciones para este suceso. En breve abordaremos esta cuestión en detalle pero, antes, quien lea esto probablemente esté experimentando (al menos) dos dudas existenciales:
• Primero y principal, ¿cuál es el color real del vestido?
• Y segundo, si tras observar el vestido de un color, intentó visualizarlo de la otra forma, es probable que no lo haya conseguido; ¿cómo puede haber gente que lo vea, entonces, de otro color? Sobre todo, teniendo en cuenta que la imagen está constituida por píxeles de colores específicos, y que es esa la información que entra en nuestras retinas. ¿Qué está ocurriendo?
La respuesta al primer interrogante es muy sencilla: el vestido real es azul y negro. No obstante, tras la popularidad que tuvieron los diseñadores como resultado de la difusión de su imagen, decidieron producir una edición limitada, en blanco y dorado. De esta forma, y como ocurre con la imagen viral, en cierto sentido, ambas respuestas son correctas.
El segundo interrogante es mucho más interesante desde un punto de vista científico, ya que pone de manifiesto una característica fundamental de la percepción: lo que percibimos no es, pura y exclusivamente, la información que nos llega a través de los sentidos, sino que el cerebro procesa esa información de diferentes formas, modificándola a partir de diversos factores (como la experiencia previa). Esto mismo se pone de manifiesto en todas las ilusiones de percepción, y es materia continua de estudio y debate en la comunidad científica.

En este caso, tan solo tres meses transcurrirían desde la viralización del vestido hasta que fuera publicado un estudio científico que arrojaría ‘algo de luz’ sobre el extraño suceso: la iluminación que nuestro cerebro infiere al observar la imagen es clave para construir nuestra percepción de sus colores. Para ver esto, los autores decidieron modificar artificialmente esta iluminación, de modo de acentuar o bien una tonalidad más azulada (como un vestido que se observa bajo la luz natural del día), o bien una más amarillenta (como ocurriría con muchas luces artificiales presentes en hogares y negocios). El resultado fue claro: la gran mayoría de las personas percibió el vestido como blanco y dorado en el primer caso, y como azul y negro en el segundo.
Profundizando en este punto, otro estudio posterior mostró que aquellas personas que son ‘alondras matutinas’ (es decir, que se levantan y acuestan más temprano de forma natural) tienen más probabilidad de interpretar la imagen como un vestido blanco y dorado. En cambio, los ‘búhos nocturnos’ –personas que se levantan y acuestan bien tarde– lo perciben azul y negro, en concordancia con la iluminación artificial a la que están más acostumbrados.
Y si todavía tiene dificultad para creer que el vestido puede ser percibido de una forma totalmente diferente, la siguiente imagen puede que acabe por convencerlo. A la derecha, tenemos un vestido blanco y dorado, pero con una mitad bajo una sombra azulada; a la izquierda, el mismo vestido, esta vez azul y negro, con una mitad bajo una luz amarilla. Las líneas horizontales nos muestran que la tonalidad amarilla en sombra azulada es equivalente a la tonalidad negra en luz amarilla y, de igual forma, la tonalidad blanca en sombra azulada resulta idéntica a aquella azul en luz amarilla.

Esto pone de manifiesto cómo, con las mismas tonalidades, es posible tener dos interpretaciones totalmente diferentes, en función del contexto circundante. Más aún, si bien uno puede estar completamente seguro de su forma de ver las cosas, puede acabar sorprendiéndose al descubrir que otras personas lo ven de una forma por demás diferente, y que, en muchos casos, ambas interpretaciones pueden ser acertadas.
Soluciones
Enmendando reglas
La regla es n3 − 5n2 + 10n − 4.
No hace falta enmendar reglas
a) Si rota la revista, verá los números: 86, X, 88, 89, 90, y ahora puede poner cualquiera de los infinitos números posibles en lugar de la X. Si se lo preguntan en un test psicológico, por ejemplo para renovar el carnet de conducir, le sugiero fuertemente que diga el 87.
b) Sigue el 4 (y luego un 6, otro 4, otro 6, indefinidamente). Esto siempre y cuando cada número indique la cantidad de letras del anterior. Pero no me extrañaría que alguien que se dedique a la estadística haga regresión lineal, redondee, y concluya que el 5 es el siguiente entero. Y si recalcula agregando ese valor, aparecerá otro 5, y así indefinidamente. Bueno, la recontrabanco: 5 tiene cinco letras… la regla de la cantidad de letras del anterior se cumple con una única excepción, nada mal. Mucho peor es ‘overfitear’ interpolando. ¡Eso nunca!
Equipo de la sección ‘Ilusiones y juegos matemáticos’
Federico Barrera Lemarchand
Físico, UTDT, UBA-Conicet.
[email protected]
Marilina Carena
Matemática, UNL-Conicet.
[email protected]
Giulia Solange Clas
Bióloga, INEU, FLENI-Conicet.
[email protected]
Nicolás Fernández Larrosa
Biólogo, IFIBYNE, UBA-Conicet.
[email protected]
Pablo Groisman
Matemático, UBA-Conicet.
[email protected]
Matías López-Rosenfeld
Computador, UBA-Conicet.
[email protected]
Mariano I Martínez (coordinador)
Biólogo, MACN-Conicet.
[email protected]
Juan Pablo Pinasco
Matemático, UBA-Conicet.
[email protected]
Nicolás Pírez (coordinador)
Neurobiólogo, IFIBYNE, UBA-Conicet.
[email protected]
Alfredo Sanzo
Ingeniero, UTN, UBA-Conicet.
[email protected]
Nicolás Sirolli
Matemático, UBA-Conicet.
[email protected]
Preguntas, comentarios y sugerencias:
[email protected]











